1차원 Bin Packing 알고리즘을 활용한 작업 배분 최적화_1.개요

이 글에서는 1차원 Bin Packing의 개념과 알고리즘에 대해서 살펴보고 이를 이용하여 최소의 작업그룹수와 최소의 실행시간을 목표로 최적화할 수 있는 방법을 알아본다. 또한, 필자가 Excel VBA로 직접 구현한 1차원 Bin Packing 도구에 대해 소개하고, Python에서 제공되는 package를 이용하는 사례에 대해 살펴본다.

Excel VBA로 구현한 도구의 소스코드와 Python으로 구현한 예시는 아래 링크에서 확인할수 있다.

Link: https://github.com/DAToolset/1D-bin-packing

1. 최적화 알고리즘 1차원 Bin Packing 개요

1.1. Bin Packing의 필요성

다음과 같은 경우를 생각해 보자.

Case 1)

Database 서버 A와 B가 있는 환경이다. A 는 약 3천개의 테이블을 관리하며 현재 운영중인 서버이고, B는 새로 만들어져서 아무것도 없이 비어있는 서버이다. A서버의 데이터는 총 6TB에 달한다. 제약된 시간(예: 6시간) 내에 A서버의 대상 테이블 데이터를 추출하여 B서버로 전달하고자 한다. 가능한 빠른 시간 내에 데이터 추출을 완료하려면 테이블들을 몇 개의 그룹으로 나누고 각 그룹에 어떤 테이블을 배치해야 원하는 결과를 얻을 수 있을까? 이 작업은 매월 1회 이상 주기적으로 실행해야 한다. 매 실행 때마다 A 서버에는 신규 테이블이 추가될 수 있고, 각 테이블의 데이터 양은 늘어나거나 줄어들 수 있다.

Case 2)

5천여개의 Job(Procedure 또는 SQL 등)들이 있다. 각 Job의 순서 또는 의존성(Dependency)이 없다고 할 때, 전체 실행시간을 최소화하려면 Job들을 몇 개의 그룹으로 나누고 어떤 Job을 어떤 그룹에 배치해야 할까?

위의 Case와 같이 수백 개, 수 천개 이상의 item을 가지고 최적 조합을 찾아내는 과정을 사람이 수작업으로 시도하기에는 상당한 시간과 노력이 필요하다. 만약 수작업으로 어떤 작업 그룹의 조합을 찾았다고 하더라도 그 조합이 최적인지 확인하기는 것은 그리 간단한 문제가 아니다.

Bin Packing 알고리즘이 필요한 이유는 최소의 투자로 최대의 효과를 내는 경제적인 이유 때문이다. Bin Packing 알고리즘은 제약된 시간 내에 또는 제약된 공간 내에 최대한 많이 채울 수 있는 최적 조합을 찾아내야 할 때 범용적으로 사용할 수 있다.

1.2. Bin Packing 개념

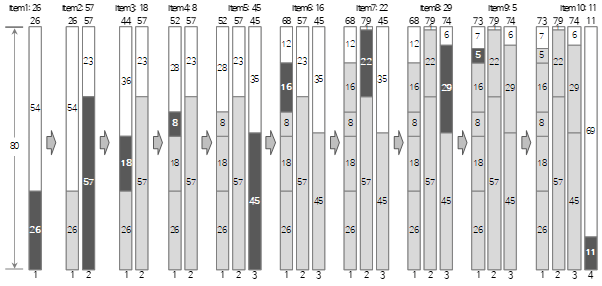
Bin Packing은 여러 항목(Item)들을 Bin에 최대한 많이 채우기 위해 몇 개의 Bin이 필요한지 알아내는 최적화 알고리즘이다. 입력 값은 두 가지이다. 첫 번째는 한 Bin의 크기, 두 번째는 Item의 목록이다. Item의 목록은 이름과 크기로 구성하는데, 이름은 선택적으로 입력한다. 출력 값은 최적화된(가장 적은) Bin의 수, 그리고 각 Bin에 담기는 Item의 목록이다.

위의 예시 Case 1에서는 테이블의 byte수, row수, 또는 여러 차례 실행하는 경우 각 테이블의 데이터를 추출하는데 걸린 평균 시간을 크기로 볼 수 있고, Case 2에서는 각 Job의 평균 실행시간을 크기로 볼 수 있다.

 Case 2에서 “전체 실행시간을 최소화하려면”의 의미를 좀 더 살펴보자. 전체 실행시간은 각 Job이 배치된 Job 그룹의 실행 시간 중 가장 오래 걸리는 실행 시간과 같다.

즉, 전체 실행시간 = Max(Job 그룹 개별 실행시간) 이다. 다시 말해서 각 Job 그룹 실행 시간의 차이가 적어야 전체 실행 시간을 최소화할 수 있으므로, “전체 실행시간을 최소화하려면”은 “각 Job 그룹의 개별 실행시간을 거의 균등하게 하려면”과 같은 의미이다.

Bin의 크기와 Item의 크기가 길이, 시간 등 정량적인 수치 하나로 표현할 수 있을 때 1차원(1-Dimension) Bin Packing이 적용될 수 있다. 1차원 Bin Packing은 다양한 크기의 Item을 입력 받고, Bin 하나의 최대 크기를 한 가지 제약조건으로 사용하여 각 Item들을 제약조건에 맞게 배치한 결과 목록을 얻고자 하는 알고리즘이다. 입력과 제약조건, 출력에 대한 개념을 정리하면 아래와 같다.

• 입력: Item 각각의 이름과 크기 목록
• 제약조건: Bin 하나의 최대 크기
• 출력: 필요한 Bin의 개수,  각 Bin에 어떤 Item이 포함되는지에 대한 목록

크기가 2개의 수치(가로, 세로)로 표현할 수 있을 때 2차원(2-Dimension) Bin Packing, 3개의 수치(가로, 세로, 높이)로 표현할 수 있을 때 3차원(3-Dimension) Bin Packing을 적용한다. 2차원 Bin Packing은 2차원 평면에 빈 공간이 최소로 되도록 도형을 배열하거나 잘라낼 때 적용할 수 있다. 3차원 Bin Packing은 3차원 공간에 빈 공간이 적도록 항목을 쌓고자 할 때 적용할 수 있다. 3차원 Bin Packing을 적용할 수 있는 대표적인 경우는 택배 차량에 박스를 적재할 때 남는 공간이 최소화되도록 적재하는 공간 최적화이다. 2, 3차원 Bin Packing은 이 글에서는 다루지 않는다.

자세한 내용은 다음 글에 살펴보겠다.

1차원 Bin Packing 알고리즘을 활용한 작업 배분 최적화_2.알고리즘(1)

---

<< 관련 글 목록 >>

• 1차원 Bin Packing 알고리즘을 활용한 작업 배분 최적화_1.개요
• 1차원 Bin Packing 알고리즘을 활용한 작업 배분 최적화_2.알고리즘(1)
• 1차원 Bin Packing 알고리즘을 활용한 작업 배분 최적화_2.알고리즘(2)
• 1차원 Bin Packing 알고리즘을 활용한 작업 배분 최적화_3.구현(1)
• 1차원 Bin Packing 알고리즘을 활용한 작업 배분 최적화_3.구현(2)
• 1차원 Bin Packing 알고리즘을 활용한 작업 배분 최적화_4.별첨
• 1차원 Bin Packing 도구 최근 변경 사항 (2021-03-21 기준)
• 1차원 Bin Packing 알고리즘을 활용한 작업 배분 최적화 도구 설명글 전체 목차, 다운로드