Optimization of work distribution using one-dimensional bin packing algorithm_2.Algorithm(2)

2.6. Apply descending sort by Item size

So far, we have looked at the operation method and execution results of each algorithm of Next Fit, First Fit, Worst Fit, and Best Fit. The results are different when processing in random order when the size of the input data is not arranged in a certain order and processing in a sorted state. Since filling large-sized items first usually yields good results, you can think of a method of sorting items in descending order first and then processing them.

First, the input data and the data sorted in descending order are as follows.

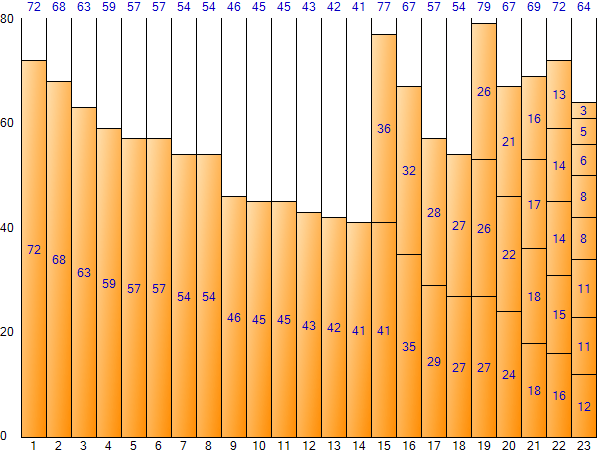
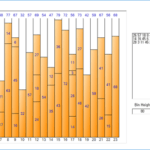
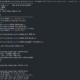
# Input Data 26 57 18 8 45 16 22 29 5 11 8 27 54 13 17 21 63 14 16 45 6 32 57 24 18 27 54 35 12 43 36 72 14 28 3 11 46 27 42 59 6 186

# Sort in descending order Input data 72 68 63 59 57 57 54 54 46 45 45 43 42 41 41 36 35 32 29 28 27 27 27 26 26 24 22 21 18 18 17 16 16 15 14 14 14 18 13 12

Let's take a look at the results of running each algorithm with data sorted in descending order as input.

2.7. Next Fit with descending sort

The total space is 1,840 (size of each bin 80 * number of bins 23), the remaining space total is 488, and the space inefficiency is about 26.52% (488/1,840).

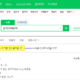
2.8. First Fit with Descending Sort

The total space is 1,440 (size of each bin 80 * number of bins 18), the remaining space total is 88, and the space inefficiency is about 6.11% (88/1,440).

2.9. Worst Fit with Descending Sort

The total space is 1,440 (size of each bin 80 * number of bins 18), the remaining space total is 88, and the space inefficiency is about 6.11% (88/1,440).

2.10. Best Fit with Descending Sort

The total space is 1,440 (size of each bin 80 * number of bins 18), the remaining space total is 88, and the space inefficiency is about 6.11% (88/1,440).

2.11. Comparison of algorithm application results

 In the case examined above, except for Next Fit, which has the largest inefficiency, the results of the remaining space sum and space inefficiency of First Fit, Worst Fit, and Best Fit are all the same, and the items filled in each bin are configured differently.

For reference, the same result is a coincidence caused by the input data and constraints in this example. If the input data and constraints are different, the residual space sum, space inefficiency, item composition list of bins, etc. may be different.

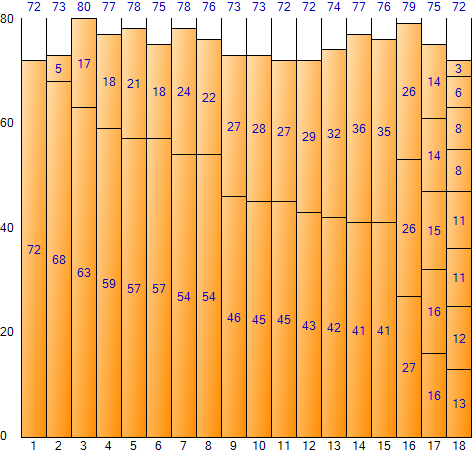
The comparison of the unsorted and sorted results is as follows.

▼ Next Fit

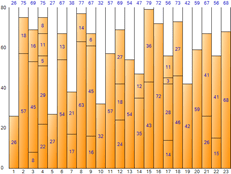
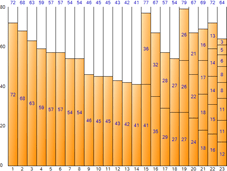
▼ First Fit

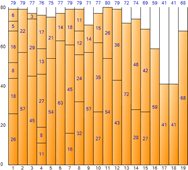
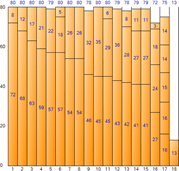
▼ Worst Fit

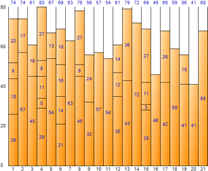
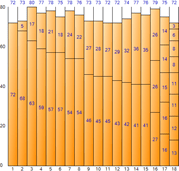
▼ Best Fit

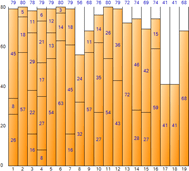
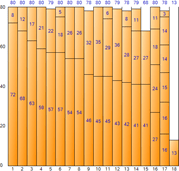
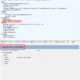
Below is the quantitative information yielded from the execution of each algorithm.

algorithm	Item	before sorting	After sorting	compare
Next Fit	number of comparisons	44	44	no change
	total space	1,840	1,840
	Sum Remaining Space	488	488
	space inefficiency	26.525	26.525
First Fit	number of comparisons	330	448	The number of comparisons increased, but space inefficiency decreased and improved
	total space	1,520	1,440
	Sum Remaining Space	168	88
	space inefficiency	11.05%	6.11%
Worst Fit	number of comparisons	465	643
	total space	1,680	1,440
	Sum Remaining Space	328	88
	space inefficiency	19.52%	6.11%
Best Fit	number of comparisons	428	643
	total space	1,520	1,440
	Sum Remaining Space	168	88
	space inefficiency	11.05%	6.11%

The number of comparisons in the table above is an approximate measurement by the Excel VBA-based tool, which will be introduced next. Looking at the above, you can see that the result of Bin Packing after sorting in descending order by item size reduces space inefficiency and is more densely packed. Through this, it can be seen that sorting first and applying the algorithm can obtain more optimized results.

Best Fit is not always optimal. It is advisable to examine the results of each algorithm run and select the optimal result for the situation at the time.

---

So far, we have looked at the Bin Packing algorithm in detail. Next, we look at tools that implement this algorithm.

---

<< List of related articles >>

• Optimization of work distribution using one-dimensional bin packing algorithm_1.Overview
• Optimization of work distribution using one-dimensional bin packing algorithm_2.Algorithm (1)
• Optimization of work distribution using one-dimensional bin packing algorithm_2.Algorithm(2)
• Optimization of work distribution using one-dimensional bin packing algorithm_3.Implementation (1)
• Optimization of work distribution using one-dimensional bin packing algorithm_3.Implementation (2)
• Optimization of work distribution using one-dimensional bin packing algorithm_4.Attachment
• One-dimensional Bin Packing Tool Recent Changes (as of March 21, 2021)
• Work distribution optimization tool using one-dimensional bin packing algorithm Full Contents, Download