Optimization of work distribution using one-dimensional bin packing algorithm_1.Overview
In this article, we will look at the concept and algorithm of one-dimensional bin packing and find out how to optimize it with the goal of the minimum number of workgroups and the minimum execution time using it. In addition, I will introduce the one-dimensional Bin Packing tool that I directly implemented with Excel VBA, and look at the case of using the package provided in Python.
The source code of the tool implemented in Excel VBA and examples implemented in Python can be found at the link below.
Link: https://github.com/DAToolset/1D-bin-packing
1. Overview of Optimization Algorithm One-Dimensional Bin Packing
1.1. The Need for Bin Packing
Consider the following case.
Case 1)
It is an environment with database servers A and B. A is a server that manages about 3,000 tables and is currently running, and B is a newly created and empty server. Server A has a total of 6TB of data. We want to extract the target table data of server A within a limited time (eg 6 hours) and deliver it to server B. In order to complete the data extraction as quickly as possible, how many groups should the tables be divided into and which tables should be placed in each group to achieve the desired result? This task should be run periodically, at least once a month. A new table can be added to server A for every execution, and the amount of data in each table can be increased or decreased.
Case 2)
There are about 5,000 Jobs (Procedure or SQL, etc.). Assuming that there is no order or dependency of each job, in order to minimize the overall execution time, how many groups should the Jobs be divided and which Jobs should be placed in which group?
As in the case above, it takes a considerable amount of time and effort for a person to manually try to find the optimal combination of hundreds or thousands of items. Even if a combination of a certain work group is found manually, it is not a simple matter to confirm whether that combination is optimal.
The reason that the Bin Packing algorithm is needed is for economic reasons that provide maximum effect with minimum investment. The bin packing algorithm can be used universally when it is necessary to find the optimal combination that can be filled as much as possible within a constrained time or within a constrained space.
1.2. Bin Packing Concept
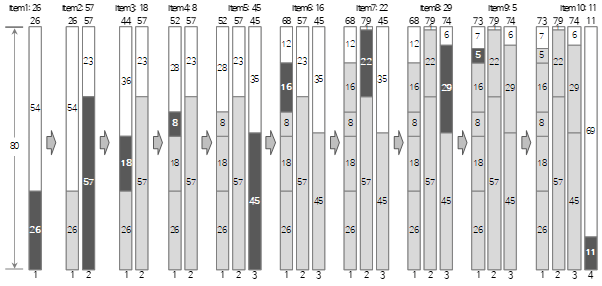
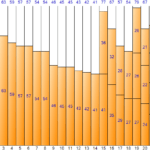
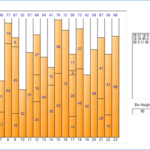
Bin Packing is an optimization algorithm that finds out how many bins are needed to fill a bin with as many items as possible. There are two input values. The first is the size of one bin, and the second is a list of items. The list of items consists of a name and a size, and the name is optionally entered. The output value is the number of optimized (least) bins and a list of items to be included in each bin.
In the above example Case 1, the number of bytes of the table, the number of rows, or the average time taken to extract the data of each table when executing multiple times can be viewed as the size. In Case 2, the average execution time of each job can be viewed as the size. can
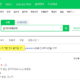
Let's take a closer look at the meaning of "to minimize the total execution time" in Case 2. The total execution time is the same as the longest execution time among the execution times of the job group in which each job is placed.
That is, the total execution time = Max (Job group individual execution time). In other words, since the total execution time can be minimized only when the difference in execution time of each job group is small, “to minimize the overall execution time” is the same as “to make the individual execution time of each job group almost equal”.
When the size of a bin and the size of an item can be expressed in one quantitative number such as length and time, 1-dimensional bin packing can be applied. One-dimensional bin packing is an algorithm that receives items of various sizes and uses the maximum size of one bin as one constraint to obtain a list of results by arranging each item according to the constraint. The concepts of input, constraint, and output are summarized below.
- Input: A list of each item's name and size
- Constraint: Maximum size of one bin
- Output: the number of bins required, a list of which items each bin contains
2-Dimension Bin Packing when the size can be expressed in two numbers (width, height) and 3-Dimension Bin Packing when it can be expressed in three numbers (width, height, height) apply 2D Bin Packing can be applied when arranging or cutting out figures so that the empty space on the 2D plane is minimized. 3D Bin Packing can be applied when you want to stack items so that there is little empty space in 3D space. A typical case where three-dimensional bin packing can be applied is space optimization in which the remaining space is minimized when loading boxes in a delivery vehicle. 2 and 3D bin packing is not covered in this article.
We will see more details in the next article.
Optimization of work distribution using one-dimensional bin packing algorithm_2.Algorithm (1)
<< List of related articles >>
- Optimization of work distribution using one-dimensional bin packing algorithm_1.Overview
- Optimization of work distribution using one-dimensional bin packing algorithm_2.Algorithm (1)
- Optimization of work distribution using one-dimensional bin packing algorithm_2.Algorithm(2)
- Optimization of work distribution using one-dimensional bin packing algorithm_3.Implementation (1)
- Optimization of work distribution using one-dimensional bin packing algorithm_3.Implementation (2)
- Optimization of work distribution using one-dimensional bin packing algorithm_4.Attachment
- One-dimensional Bin Packing Tool Recent Changes (as of March 21, 2021)
- Work distribution optimization tool using one-dimensional bin packing algorithm Full Contents, Download