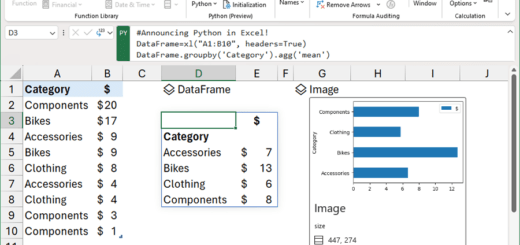
Optimization of work distribution using one-dimensional bin packing algorithm_3.Implementation (2)

3.2. Leverage the Python Bin Packing package

3.2.1. Introduction and installation of the Python Bin Packing package

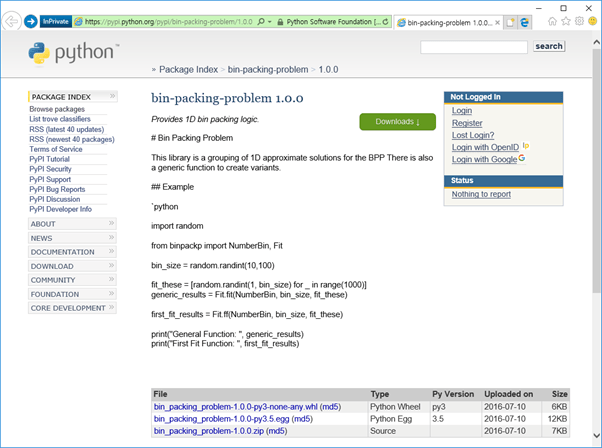
Bin Packing packages that can be utilized in Python can be found on the Pypi (Python Package Index) web page. https://pypi.python.org/pypi/bin-packing-problem/1.0.0 provided by You can refer to the brief description and example source code of the Bin Packing package at this URL, and you can check the implemented source code by downloading the package file.

Within the Fit module of this package, the following Bin Packing implementation method is provided.

algorithm	method (no sort applied)	method (applies sorting)
Next Fit	nf	– (not implemented in v1.0)
First Fit	ff	ffd
Worst Fit	wf	wfd
Best Fit	bf	bfd

Installation uses the Python package manager pip as follows.

pip install bin-packing-problem

3.2.2. Bin Packing Sample Source Code

The following is a sample source code using the Bin Packing package installed above. The same input values used in the description of the Bin Packing algorithm in Table of Contents 2 were used.

For reference, I don't know if it's the intention of the package developer or a mistake, but the nfd (next fit descending) method is not implemented, so it's commented out.

from binpackp import NumberBin, Fit

def print_result(fit_name, fit_result):
    print(fit_name + " Result: ", fit_result)
    for bin in fit_result.bins:
        print(bin)
    print()

bin_size = 80
fit_these = [26, 57, 18, 8, 45, 16, 22, 29, 5, 11, 8, 27, 54, 13, 17, 21, 63, 14, 16, 45, 6, 32, 57, 24, 18, 27, 54, 35, 12, 43, 36, 72, 14, 28, 3, 11, 46, 27, 42, 59, 26, 41, 15, 41, 68]

next_fit_results = Fit.nf(NumberBin, bin_size, fit_these)
first_fit_results = Fit.ff(NumberBin, bin_size, fit_these)
worst_fit_result = Fit.wf(NumberBin, bin_size, fit_these)
best_fit_result = Fit.bf(NumberBin, bin_size, fit_these)

# sorted_next_fit_results = Fit.nfd(NumberBin, bin_size, fit_these) # not implemented
sorted_first_fit_results = Fit.ffd(NumberBin, bin_size, fit_these)
sorted_worst_fit_result = Fit.wfd(NumberBin, bin_size, fit_these)
sorted_best_fit_result = Fit.bfd(NumberBin, bin_size, fit_these)

print_result("Next Fit", next_fit_results)
print_result("First Fit", first_fit_results)
print_result("Worst Fit", worst_fit_result)
print_result("Best Fit", best_fit_result)

# print_result("Next Fit With Sort", next_fit_results) # not implemented
print_result("First Fit With Sort", sorted_first_fit_results)
print_result("Worst Fit With Sort", sorted_worst_fit_result)
print_result("Best Fit With Sort", sorted_best_fit_result)

3.2.3. Bin Packing sample source code output

The result of executing the sample source code is as follows. Although the execution results and output order of each algorithm described in Table of Contents 2 are different, the contents filled in are the same.

Next Fit Result:  <BPResult (Total Bins: 23, Total Volume: 1840, Unused Volume: 488)>
<NumberBin>(Volume: 26/80, Items: [26])
<NumberBin>(Volume: 75/80, Items: [57, 18])
<NumberBin>(Volume: 69/80, Items: [8, 45, 16])
<NumberBin>(Volume: 75/80, Items: [22, 29, 5, 11, 8])
<NumberBin>(Volume: 27/80, Items: [27])
<NumberBin>(Volume: 67/80, Items: [54, 13])
<NumberBin>(Volume: 38/80, Items: [17, 21])
<NumberBin>(Volume: 77/80, Items: [63, 14])
<NumberBin>(Volume: 67/80, Items: [16, 45, 6])
<NumberBin>(Volume: 32/80, Items: [32])
<NumberBin>(Volume: 57/80, Items: [57])
<NumberBin>(Volume: 69/80, Items: [24, 18, 27])
<NumberBin>(Volume: 54/80, Items: [54])
<NumberBin>(Volume: 47/80, Items: [35, 12])
<NumberBin>(Volume: 79/80, Items: [43, 36])
<NumberBin>(Volume: 72/80, Items: [72])
<NumberBin>(Volume: 56/80, Items: [14, 28, 3, 11])
<NumberBin>(Volume: 73/80, Items: [46, 27])
<NumberBin>(Volume: 42/80, Items: [42])
<NumberBin>(Volume: 59/80, Items: [59])
<NumberBin>(Volume: 67/80, Items: [26, 41])
<NumberBin>(Volume: 56/80, Items: [15, 41])
<NumberBin>(Volume: 68/80, Items: [68])

First Fit Result:  <BPResult (Total Bins: 19, Total Volume: 1520, Unused Volume: 168)>
<NumberBin>(Volume: 80/80, Items: [54, 26])
<NumberBin>(Volume: 79/80, Items: [26, 18, 8, 16, 5, 6])
<NumberBin>(Volume: 79/80, Items: [57, 22])
<NumberBin>(Volume: 77/80, Items: [45, 29, 3])
<NumberBin>(Volume: 76/80, Items: [11, 8, 27, 13, 17])
<NumberBin>(Volume: 75/80, Items: [54, 21])
<NumberBin>(Volume: 77/80, Items: [63, 14])
<NumberBin>(Volume: 79/80, Items: [16, 45, 18])
<NumberBin>(Volume: 79/80, Items: [32, 24, 12, 11])
<NumberBin>(Volume: 71/80, Items: [57, 14])
<NumberBin>(Volume: 77/80, Items: [27, 35, 15])
<NumberBin>(Volume: 79/80, Items: [43, 36])
<NumberBin>(Volume: 72/80, Items: [72])
<NumberBin>(Volume: 74/80, Items: [28, 46])
<NumberBin>(Volume: 69/80, Items: [27, 42])
<NumberBin>(Volume: 59/80, Items: [59])
<NumberBin>(Volume: 41/80, Items: [41])
<NumberBin>(Volume: 41/80, Items: [41])
<NumberBin>(Volume: 68/80, Items: [68])

Worst Fit Result:  <BPResult (Total Bins: 21, Total Volume: 1680, Unused Volume: 328)>
<NumberBin>(Volume: 80/80, Items: [29, 5, 11, 8, 27])
<NumberBin>(Volume: 41/80, Items: [41])
<NumberBin>(Volume: 46/80, Items: [46])
<NumberBin>(Volume: 54/80, Items: [54])
<NumberBin>(Volume: 56/80, Items: [41, 15])
<NumberBin>(Volume: 56/80, Items: [32, 24])
<NumberBin>(Volume: 57/80, Items: [57])
<NumberBin>(Volume: 59/80, Items: [59])
<NumberBin>(Volume: 61/80, Items: [35, 12, 14])
<NumberBin>(Volume: 61/80, Items: [45, 16])
<NumberBin>(Volume: 63/80, Items: [63])
<NumberBin>(Volume: 67/80, Items: [54, 13])
<NumberBin>(Volume: 68/80, Items: [42, 26])
<NumberBin>(Volume: 68/80, Items: [68])
<NumberBin>(Volume: 69/80, Items: [28, 3, 11, 27])
<NumberBin>(Volume: 69/80, Items: [45, 6, 18])
<NumberBin>(Volume: 72/80, Items: [72])
<NumberBin>(Volume: 74/80, Items: [57, 17])
<NumberBin>(Volume: 74/80, Items: [26, 18, 8, 22])
<NumberBin>(Volume: 78/80, Items: [21, 14, 16, 27])
<NumberBin>(Volume: 79/80, Items: [43, 36])

Best Fit Result:  <BPResult (Total Bins: 19, Total Volume: 1520, Unused Volume: 168)>
<NumberBin>(Volume: 80/80, Items: [57, 18, 5])
<NumberBin>(Volume: 80/80, Items: [63, 14, 3])
<NumberBin>(Volume: 80/80, Items: [54, 26])
<NumberBin>(Volume: 79/80, Items: [26, 8, 45])
<NumberBin>(Volume: 79/80, Items: [8, 27, 17, 21, 6])
<NumberBin>(Volume: 79/80, Items: [16, 45, 18])
<NumberBin>(Volume: 79/80, Items: [54, 13, 12])
<NumberBin>(Volume: 79/80, Items: [43, 36])
<NumberBin>(Volume: 78/80, Items: [16, 22, 29, 11])
<NumberBin>(Volume: 76/80, Items: [27, 35, 14])
<NumberBin>(Volume: 74/80, Items: [28, 46])
<NumberBin>(Volume: 74/80, Items: [59, 15])
<NumberBin>(Volume: 72/80, Items: [72])
<NumberBin>(Volume: 69/80, Items: [27, 42])
<NumberBin>(Volume: 68/80, Items: [57, 11])
<NumberBin>(Volume: 68/80, Items: [68])
<NumberBin>(Volume: 56/80, Items: [32, 24])
<NumberBin>(Volume: 41/80, Items: [41])
<NumberBin>(Volume: 41/80, Items: [41])

First Fit With Sort Result:  <BPResult (Total Bins: 18, Total Volume: 1440, Unused Volume: 88)>
<NumberBin>(Volume: 80/80, Items: [45, 35])
<NumberBin>(Volume: 80/80, Items: [54, 26])
<NumberBin>(Volume: 80/80, Items: [54, 26])
<NumberBin>(Volume: 80/80, Items: [59, 21])
<NumberBin>(Volume: 80/80, Items: [63, 17])
<NumberBin>(Volume: 80/80, Items: [68, 12])
<NumberBin>(Volume: 80/80, Items: [72, 8])
<NumberBin>(Volume: 80/80, Items: [45, 29, 6])
<NumberBin>(Volume: 80/80, Items: [57, 18, 5])
<NumberBin>(Volume: 79/80, Items: [57, 22])
<NumberBin>(Volume: 78/80, Items: [46, 32])
<NumberBin>(Volume: 79/80, Items: [43, 36])
<NumberBin>(Volume: 78/80, Items: [42, 28, 8])
<NumberBin>(Volume: 79/80, Items: [41, 27, 11])
<NumberBin>(Volume: 79/80, Items: [41, 27, 11])
<NumberBin>(Volume: 72/80, Items: [27, 24, 18, 3])
<NumberBin>(Volume: 75/80, Items: [16, 16, 15, 14, 14])
<NumberBin>(Volume: 13/80, Items: [13])

Worst Fit With Sort Result:  <BPResult (Total Bins: 18, Total Volume: 1440, Unused Volume: 88)>
<NumberBin>(Volume: 80/80, Items: [63, 17])
<NumberBin>(Volume: 72/80, Items: [13, 12, 11, 11, 8, 8, ...])
<NumberBin>(Volume: 72/80, Items: [45, 27])
<NumberBin>(Volume: 72/80, Items: [43, 29])
<NumberBin>(Volume: 72/80, Items: [72])
<NumberBin>(Volume: 73/80, Items: [68, 5])
<NumberBin>(Volume: 73/80, Items: [46, 27])
<NumberBin>(Volume: 73/80, Items: [45, 28])
<NumberBin>(Volume: 74/80, Items: [42, 32])
<NumberBin>(Volume: 75/80, Items: [16, 16, 15, 14, 14])
<NumberBin>(Volume: 75/80, Items: [57, 18])
<NumberBin>(Volume: 76/80, Items: [54, 22])
<NumberBin>(Volume: 76/80, Items: [41, 35])
<NumberBin>(Volume: 77/80, Items: [59, 18])
<NumberBin>(Volume: 77/80, Items: [41, 36])
<NumberBin>(Volume: 78/80, Items: [57, 21])
<NumberBin>(Volume: 78/80, Items: [54, 24])
<NumberBin>(Volume: 79/80, Items: [27, 26, 26])

Best Fit With Sort Result:  <BPResult (Total Bins: 18, Total Volume: 1440, Unused Volume: 88)>
<NumberBin>(Volume: 80/80, Items: [45, 35])
<NumberBin>(Volume: 80/80, Items: [54, 26])
<NumberBin>(Volume: 80/80, Items: [54, 26])
<NumberBin>(Volume: 80/80, Items: [59, 21])
<NumberBin>(Volume: 80/80, Items: [63, 17])
<NumberBin>(Volume: 80/80, Items: [68, 12])
<NumberBin>(Volume: 80/80, Items: [27, 24, 18, 11])
<NumberBin>(Volume: 80/80, Items: [72, 8])
<NumberBin>(Volume: 80/80, Items: [45, 29, 6])
<NumberBin>(Volume: 80/80, Items: [57, 18, 5])
<NumberBin>(Volume: 79/80, Items: [43, 36])
<NumberBin>(Volume: 79/80, Items: [57, 22])
<NumberBin>(Volume: 79/80, Items: [41, 27, 11])
<NumberBin>(Volume: 78/80, Items: [46, 32])
<NumberBin>(Volume: 78/80, Items: [42, 28, 8])
<NumberBin>(Volume: 78/80, Items: [16, 16, 15, 14, 14, 3])
<NumberBin>(Volume: 68/80, Items: [41, 27])
<NumberBin>(Volume: 13/80, Items: [13])

4. Future development direction and reference materials

The Bin Packing algorithm examined so far is composed of the premise that each item is independent without any relation to each other. In other words, it is an algorithm that does not consider dependencies, such as when items need to be filled together in one bin because there is a precedence relationship between items.

In reality, it can be said that there are far more cases where dependencies exist than cases where there are no dependencies. For example, in practice, there are more cases where Job2 and Job3 should be executed after Job1 is executed first, rather than a case where Job1, Job2, and Job3 can be executed independently.

It is necessary to develop the Bin Packing algorithm known so far by reflecting its dependencies. In this article, we did not look at Bin Packing that reflects dependencies. I would be very grateful if anyone could share what they have improved or developed through further research.

Feedback on the contents of this article is a comment or https://github.com/DAToolset/1D-bin-packing github issue, please send it to my email.

---

<< List of related articles >>

• Optimization of work distribution using one-dimensional bin packing algorithm_1.Overview
• Optimization of work distribution using one-dimensional bin packing algorithm_2.Algorithm (1)
• Optimization of work distribution using one-dimensional bin packing algorithm_2.Algorithm(2)
• Optimization of work distribution using one-dimensional bin packing algorithm_3.Implementation (1)
• Optimization of work distribution using one-dimensional bin packing algorithm_3.Implementation (2)
• Optimization of work distribution using one-dimensional bin packing algorithm_4.Attachment
• One-dimensional Bin Packing Tool Recent Changes (as of March 21, 2021)
• Work distribution optimization tool using one-dimensional bin packing algorithm Full Contents, Download