Optimización de la distribución del trabajo mediante el algoritmo bin packing unidimensional_3.Implementación (2)
3.2. Aproveche el paquete Python Bin Packing
3.2.1. Introducción e instalación del paquete Python Bin Packing
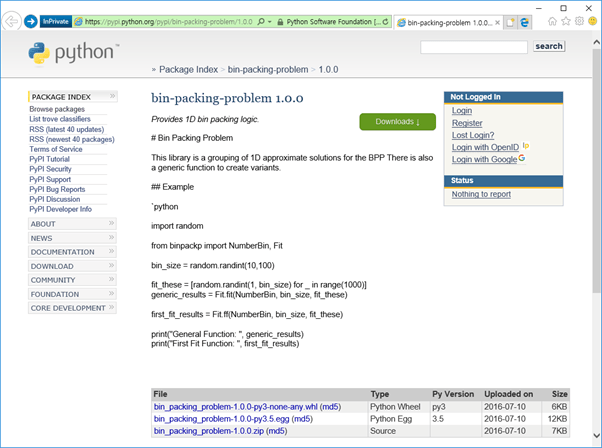
Los paquetes de Bin Packing disponibles en Python se enumeran en la página web de Pypi (Python Package Index). https://pypi.python.org/pypi/bin-packing-problem/1.0.0 proporcionado por Desde esta URL, puede consultar la breve descripción y el código fuente de ejemplo del paquete Bin Packing, y puede descargar el archivo del paquete para verificar el código fuente implementado.
El método que implementa el siguiente empaque en contenedores se proporciona en el módulo Ajustar de este paquete.
| algoritmo | método (sin ordenación aplicada) | método (aplicar clasificación) |
| Siguiente ajuste | nf | – (no implementado en v1.0) |
| primer ajuste | f | ffd |
| peor ajuste | wf | wfd |
| Mejor ajuste | novio | bdf |
La instalación usa pip, el administrador de paquetes de Python, de la siguiente manera.
pip install bin-packing-problema3.2.2. Código fuente de muestra de embalaje de contenedores
El siguiente es un código fuente de muestra que utiliza el paquete Bin Packing instalado anteriormente. Se utilizaron los mismos valores de entrada utilizados en la descripción del algoritmo Bin Packing en la Tabla 2.
Como referencia, no sé si es la intención del desarrollador del paquete o un error, pero el método nfd (siguiente ajuste descendente) no está implementado y está comentado.
from binpackp import NumberBin, Fit
def print_result(fit_name, fit_result):
print(fit_name + " Result: ", fit_result)
for bin in fit_result.bins:
print(bin)
print()
bin_size = 80
fit_these = [26, 57, 18, 8, 45, 16, 22, 29, 5, 11, 8, 27, 54, 13, 17, 21, 63, 14, 16, 45, 6, 32, 57, 24, 18, 27, 54, 35, 12, 43, 36, 72, 14, 28, 3, 11, 46, 27, 42, 59, 26, 41, 15, 41, 68]
next_fit_results = Fit.nf(NumberBin, bin_size, fit_these)
first_fit_results = Fit.ff(NumberBin, bin_size, fit_these)
worst_fit_result = Fit.wf(NumberBin, bin_size, fit_these)
best_fit_result = Fit.bf(NumberBin, bin_size, fit_these)
# sorted_next_fit_results = Fit.nfd(NumberBin, bin_size, fit_these) # not implemented
sorted_first_fit_results = Fit.ffd(NumberBin, bin_size, fit_these)
sorted_worst_fit_result = Fit.wfd(NumberBin, bin_size, fit_these)
sorted_best_fit_result = Fit.bfd(NumberBin, bin_size, fit_these)
print_result("Next Fit", next_fit_results)
print_result("First Fit", first_fit_results)
print_result("Worst Fit", worst_fit_result)
print_result("Best Fit", best_fit_result)
# print_result("Next Fit With Sort", next_fit_results) # not implemented
print_result("First Fit With Sort", sorted_first_fit_results)
print_result("Worst Fit With Sort", sorted_worst_fit_result)
print_result("Best Fit With Sort", sorted_best_fit_result)
3.2.3. Salida de código fuente de muestra de embalaje de contenedores
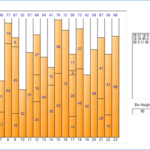
El resultado de ejecutar el código fuente de ejemplo es el siguiente. Aunque el resultado de la ejecución y el orden de salida de cada algoritmo descrito en la Tabla 2 son diferentes, se puede ver que los contenidos rellenados son los mismos.
Next Fit Result: <BPResult (Total Bins: 23, Total Volume: 1840, Unused Volume: 488)> <NumberBin>(Volume: 26/80, Items: [26]) <NumberBin>(Volume: 75/80, Items: [57, 18]) <NumberBin>(Volume: 69/80, Items: [8, 45, 16]) <NumberBin>(Volume: 75/80, Items: [22, 29, 5, 11, 8]) <NumberBin>(Volume: 27/80, Items: [27]) <NumberBin>(Volume: 67/80, Items: [54, 13]) <NumberBin>(Volume: 38/80, Items: [17, 21]) <NumberBin>(Volume: 77/80, Items: [63, 14]) <NumberBin>(Volume: 67/80, Items: [16, 45, 6]) <NumberBin>(Volume: 32/80, Items: [32]) <NumberBin>(Volume: 57/80, Items: [57]) <NumberBin>(Volume: 69/80, Items: [24, 18, 27]) <NumberBin>(Volume: 54/80, Items: [54]) <NumberBin>(Volume: 47/80, Items: [35, 12]) <NumberBin>(Volume: 79/80, Items: [43, 36]) <NumberBin>(Volume: 72/80, Items: [72]) <NumberBin>(Volume: 56/80, Items: [14, 28, 3, 11]) <NumberBin>(Volume: 73/80, Items: [46, 27]) <NumberBin>(Volume: 42/80, Items: [42]) <NumberBin>(Volume: 59/80, Items: [59]) <NumberBin>(Volume: 67/80, Items: [26, 41]) <NumberBin>(Volume: 56/80, Items: [15, 41]) <NumberBin>(Volume: 68/80, Items: [68]) First Fit Result: <BPResult (Total Bins: 19, Total Volume: 1520, Unused Volume: 168)> <NumberBin>(Volume: 80/80, Items: [54, 26]) <NumberBin>(Volume: 79/80, Items: [26, 18, 8, 16, 5, 6]) <NumberBin>(Volume: 79/80, Items: [57, 22]) <NumberBin>(Volume: 77/80, Items: [45, 29, 3]) <NumberBin>(Volume: 76/80, Items: [11, 8, 27, 13, 17]) <NumberBin>(Volume: 75/80, Items: [54, 21]) <NumberBin>(Volume: 77/80, Items: [63, 14]) <NumberBin>(Volume: 79/80, Items: [16, 45, 18]) <NumberBin>(Volume: 79/80, Items: [32, 24, 12, 11]) <NumberBin>(Volume: 71/80, Items: [57, 14]) <NumberBin>(Volume: 77/80, Items: [27, 35, 15]) <NumberBin>(Volume: 79/80, Items: [43, 36]) <NumberBin>(Volume: 72/80, Items: [72]) <NumberBin>(Volume: 74/80, Items: [28, 46]) <NumberBin>(Volume: 69/80, Items: [27, 42]) <NumberBin>(Volume: 59/80, Items: [59]) <NumberBin>(Volume: 41/80, Items: [41]) <NumberBin>(Volume: 41/80, Items: [41]) <NumberBin>(Volume: 68/80, Items: [68]) Worst Fit Result: <BPResult (Total Bins: 21, Total Volume: 1680, Unused Volume: 328)> <NumberBin>(Volume: 80/80, Items: [29, 5, 11, 8, 27]) <NumberBin>(Volume: 41/80, Items: [41]) <NumberBin>(Volume: 46/80, Items: [46]) <NumberBin>(Volume: 54/80, Items: [54]) <NumberBin>(Volume: 56/80, Items: [41, 15]) <NumberBin>(Volume: 56/80, Items: [32, 24]) <NumberBin>(Volume: 57/80, Items: [57]) <NumberBin>(Volume: 59/80, Items: [59]) <NumberBin>(Volume: 61/80, Items: [35, 12, 14]) <NumberBin>(Volume: 61/80, Items: [45, 16]) <NumberBin>(Volume: 63/80, Items: [63]) <NumberBin>(Volume: 67/80, Items: [54, 13]) <NumberBin>(Volume: 68/80, Items: [42, 26]) <NumberBin>(Volume: 68/80, Items: [68]) <NumberBin>(Volume: 69/80, Items: [28, 3, 11, 27]) <NumberBin>(Volume: 69/80, Items: [45, 6, 18]) <NumberBin>(Volume: 72/80, Items: [72]) <NumberBin>(Volume: 74/80, Items: [57, 17]) <NumberBin>(Volume: 74/80, Items: [26, 18, 8, 22]) <NumberBin>(Volume: 78/80, Items: [21, 14, 16, 27]) <NumberBin>(Volume: 79/80, Items: [43, 36]) Best Fit Result: <BPResult (Total Bins: 19, Total Volume: 1520, Unused Volume: 168)> <NumberBin>(Volume: 80/80, Items: [57, 18, 5]) <NumberBin>(Volume: 80/80, Items: [63, 14, 3]) <NumberBin>(Volume: 80/80, Items: [54, 26]) <NumberBin>(Volume: 79/80, Items: [26, 8, 45]) <NumberBin>(Volume: 79/80, Items: [8, 27, 17, 21, 6]) <NumberBin>(Volume: 79/80, Items: [16, 45, 18]) <NumberBin>(Volume: 79/80, Items: [54, 13, 12]) <NumberBin>(Volume: 79/80, Items: [43, 36]) <NumberBin>(Volume: 78/80, Items: [16, 22, 29, 11]) <NumberBin>(Volume: 76/80, Items: [27, 35, 14]) <NumberBin>(Volume: 74/80, Items: [28, 46]) <NumberBin>(Volume: 74/80, Items: [59, 15]) <NumberBin>(Volume: 72/80, Items: [72]) <NumberBin>(Volume: 69/80, Items: [27, 42]) <NumberBin>(Volume: 68/80, Items: [57, 11]) <NumberBin>(Volume: 68/80, Items: [68]) <NumberBin>(Volume: 56/80, Items: [32, 24]) <NumberBin>(Volume: 41/80, Items: [41]) <NumberBin>(Volume: 41/80, Items: [41]) First Fit With Sort Result: <BPResult (Total Bins: 18, Total Volume: 1440, Unused Volume: 88)> <NumberBin>(Volume: 80/80, Items: [45, 35]) <NumberBin>(Volume: 80/80, Items: [54, 26]) <NumberBin>(Volume: 80/80, Items: [54, 26]) <NumberBin>(Volume: 80/80, Items: [59, 21]) <NumberBin>(Volume: 80/80, Items: [63, 17]) <NumberBin>(Volume: 80/80, Items: [68, 12]) <NumberBin>(Volume: 80/80, Items: [72, 8]) <NumberBin>(Volume: 80/80, Items: [45, 29, 6]) <NumberBin>(Volume: 80/80, Items: [57, 18, 5]) <NumberBin>(Volume: 79/80, Items: [57, 22]) <NumberBin>(Volume: 78/80, Items: [46, 32]) <NumberBin>(Volume: 79/80, Items: [43, 36]) <NumberBin>(Volume: 78/80, Items: [42, 28, 8]) <NumberBin>(Volume: 79/80, Items: [41, 27, 11]) <NumberBin>(Volume: 79/80, Items: [41, 27, 11]) <NumberBin>(Volume: 72/80, Items: [27, 24, 18, 3]) <NumberBin>(Volume: 75/80, Items: [16, 16, 15, 14, 14]) <NumberBin>(Volume: 13/80, Items: [13]) Worst Fit With Sort Result: <BPResult (Total Bins: 18, Total Volume: 1440, Unused Volume: 88)> <NumberBin>(Volume: 80/80, Items: [63, 17]) <NumberBin>(Volume: 72/80, Items: [13, 12, 11, 11, 8, 8, ...]) <NumberBin>(Volume: 72/80, Items: [45, 27]) <NumberBin>(Volume: 72/80, Items: [43, 29]) <NumberBin>(Volume: 72/80, Items: [72]) <NumberBin>(Volume: 73/80, Items: [68, 5]) <NumberBin>(Volume: 73/80, Items: [46, 27]) <NumberBin>(Volume: 73/80, Items: [45, 28]) <NumberBin>(Volume: 74/80, Items: [42, 32]) <NumberBin>(Volume: 75/80, Items: [16, 16, 15, 14, 14]) <NumberBin>(Volume: 75/80, Items: [57, 18]) <NumberBin>(Volume: 76/80, Items: [54, 22]) <NumberBin>(Volume: 76/80, Items: [41, 35]) <NumberBin>(Volume: 77/80, Items: [59, 18]) <NumberBin>(Volume: 77/80, Items: [41, 36]) <NumberBin>(Volume: 78/80, Items: [57, 21]) <NumberBin>(Volume: 78/80, Items: [54, 24]) <NumberBin>(Volume: 79/80, Items: [27, 26, 26]) Best Fit With Sort Result: <BPResult (Total Bins: 18, Total Volume: 1440, Unused Volume: 88)> <NumberBin>(Volume: 80/80, Items: [45, 35]) <NumberBin>(Volume: 80/80, Items: [54, 26]) <NumberBin>(Volume: 80/80, Items: [54, 26]) <NumberBin>(Volume: 80/80, Items: [59, 21]) <NumberBin>(Volume: 80/80, Items: [63, 17]) <NumberBin>(Volume: 80/80, Items: [68, 12]) <NumberBin>(Volume: 80/80, Items: [27, 24, 18, 11]) <NumberBin>(Volume: 80/80, Items: [72, 8]) <NumberBin>(Volume: 80/80, Items: [45, 29, 6]) <NumberBin>(Volume: 80/80, Items: [57, 18, 5]) <NumberBin>(Volume: 79/80, Items: [43, 36]) <NumberBin>(Volume: 79/80, Items: [57, 22]) <NumberBin>(Volume: 79/80, Items: [41, 27, 11]) <NumberBin>(Volume: 78/80, Items: [46, 32]) <NumberBin>(Volume: 78/80, Items: [42, 28, 8]) <NumberBin>(Volume: 78/80, Items: [16, 16, 15, 14, 14, 3]) <NumberBin>(Volume: 68/80, Items: [41, 27]) <NumberBin>(Volume: 13/80, Items: [13])
4. Dirección de desarrollo futuro y materiales de referencia
El algoritmo Bin Packing examinado hasta ahora se compone de la premisa de que cada elemento es independiente sin ninguna relación entre sí. En otras palabras, es un algoritmo que no considera las dependencias, como cuando los elementos deben llenarse juntos en un contenedor porque existe una relación de precedencia entre los elementos.
En realidad, se puede decir que hay muchos más casos en los que existen dependencias que casos en los que no hay dependencias. Por ejemplo, hay más casos en la práctica en los que Job2 y Job3 deben ejecutarse después de que Job1 se ejecute primero, en lugar del caso en el que Job1, Job2 y Job3 pueden ejecutarse de forma independiente.
Es necesario desarrollar el algoritmo Bin Packing conocido hasta ahora reflejando sus dependencias. En este artículo, no analizamos el Bin Packing que refleja las dependencias. Estaría muy agradecido si alguien pudiera compartir lo que ha mejorado o desarrollado a través de investigaciones adicionales.
La retroalimentación sobre el contenido de este artículo es un comentario o https://github.com/DAToolset/1D-bin-packing Problema de github, por favor envíelo a mi correo electrónico.
<< Lista de artículos relacionados >>
- Optimización de la distribución del trabajo utilizando un algoritmo de empaque de contenedores unidimensional_1.Descripción general
- Optimización de la distribución del trabajo mediante bin packing algorítmico unidimensional_2.Algoritmo (1)
- Optimización de la distribución del trabajo utilizando bin packing unidimensional algoritmo_2.Algoritmo(2)
- Optimización de la distribución del trabajo mediante el algoritmo bin packing unidimensional_3.Implementación (1)
- Optimización de la distribución del trabajo mediante el algoritmo bin packing unidimensional_3.Implementación (2)
- Optimización de la distribución del trabajo utilizando un algoritmo de empaque de contenedores unidimensional_4.Adjunto
- Cambios recientes de la herramienta de embalaje de contenedores unidimensionales (al 21 de marzo de 2021)
- Herramienta de optimización de la distribución del trabajo utilizando un algoritmo de empaque de contenedores unidimensional. Contenido completo, Descargar