Optimización de la distribución del trabajo mediante bin packing algorítmico unidimensional_2.Algoritmo (1)
2. Algoritmo de embalaje de contenedores unidimensional
2.1. Tipo de algoritmo de embalaje de bin unidimensional
Los cuatro algoritmos representativos de Bin Packing son los siguientes.
- Siguiente ajuste: rellene el último contenedor o el nuevo contenedor
- First Fit: busque y llene siempre desde el primer contenedor
- Peor ajuste: encuentre y llene el contenedor que puede llenar el elemento actual con el tamaño restante más grande entre todos los contenedores
- Mejor ajuste: encuentre y llene el contenedor que puede llenar el elemento actual con el tamaño restante más pequeño entre todos los contenedores.
Además, se puede obtener un resultado mucho más optimizado ordenando todo el Item en orden descendente de tamaño y aplicando cada algoritmo. Considerando el método de aplicar el ordenamiento descendente, se puede decir que hay un total de 8 algoritmos.
Las siguientes entradas y restricciones se utilizan para la explicación. (Se omite el nombre del artículo en la entrada y solo se describe el tamaño)
- Entrada: 26 57 18 8 45 16 22 29 5 11 8 27 54 13 17 21 63 14 16 45 6 32 57 24 18 27 54 35 12 43 36 72 14 28 3 11 46 27 42 59 26 41 6 15
- Restricción: 80 (tamaño máximo de un contenedor)
Nota: Los datos y las restricciones de este caso son http://www.developerfusion.com/article/5540/bin-packing/ Los datos básicos de la aplicación de muestra de embalaje de contenedores que se pueden descargar de . La pantalla de esta aplicación de ejemplo es la siguiente.
Echemos un vistazo detallado al pseudocódigo, el proceso de procesamiento y el resultado de la ejecución de cada algoritmo.
2.2. Siguiente algoritmo de ajuste
Para cada artículo, se llena el último contenedor si se puede llenar, y si no se puede llenar, se crea y llena un nuevo contenedor. Next Fit es el más sencillo, pero el resultado no es óptimo.
// Pseudo code
item(1)을 새로운 Bin(1)에 채운다.
for (i=2; i<=item 개수; i++) {
j = 마지막 Bin index
if (item(i).Size <= Bin(j).남은공간Size) {
Bin(j)에 item(i)를 채운다;
}
else {
새로운 Bin(j+1)을 생성하고 item(i)를 채운다;
}
}
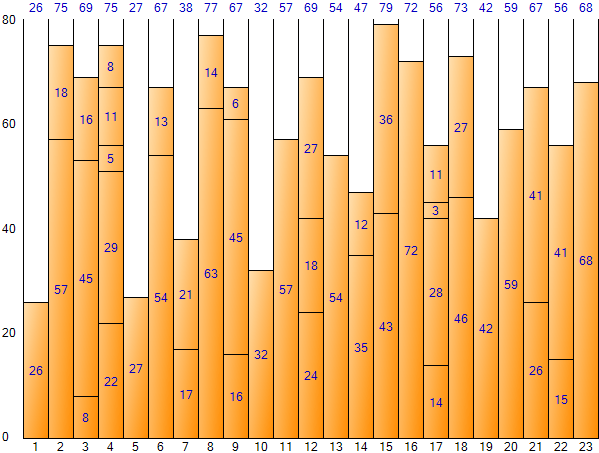
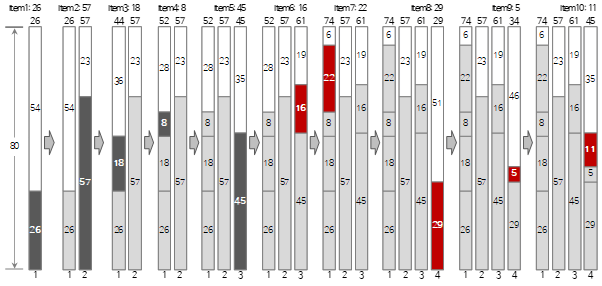
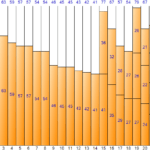
Echemos un vistazo al proceso hasta el <10> de los valores de entrada anteriores en la figura a continuación.
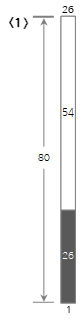
El primer valor de entrada <26> crea un nuevo Bin1 y lo llena.
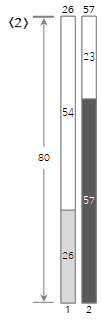
Dado que el segundo valor de entrada <57> es mayor que el tamaño restante (54) de Bin(1) y no se puede llenar, se crea y llena un nuevo Bin(2).
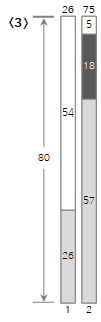
El tercer valor de entrada <18> es más pequeño que el tamaño restante (23) del contenedor actual (2), por lo que se llena en el contenedor (2).
Dado que el cuarto valor de entrada <8> es mayor que el tamaño restante (5) del contenedor actual (2) y no se puede llenar, se crea y llena un nuevo contenedor (3). Como puede ver aquí, el método Next Fit no utiliza los contenedores que ya han pasado, incluso si todavía queda espacio. Por lo tanto, se puede desperdiciar mucho espacio.
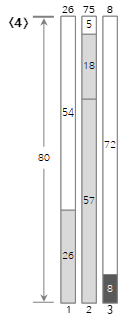
El quinto valor de entrada <45> es más pequeño que el tamaño restante (72) del contenedor actual (3), por lo que se llena en el contenedor (3).
El sexto valor de entrada <16> es más pequeño que el tamaño restante (27) del contenedor actual (3), por lo que se llena en el contenedor (3).
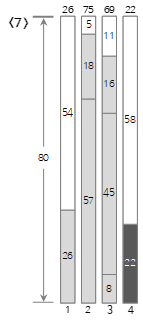
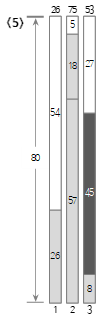
Dado que el séptimo valor de entrada <22> es mayor que el tamaño restante de Bin(3) (11) y no se puede llenar, se crea y llena un nuevo Bin(4).
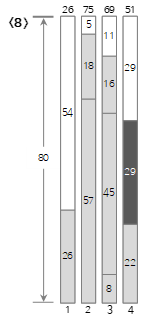
El octavo valor de entrada <29> es más pequeño que el tamaño restante (58) del contenedor actual (4), por lo que se llena en el contenedor (4).
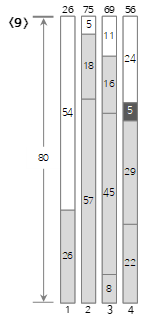
El noveno valor de entrada <5> es más pequeño que el tamaño restante (29) del contenedor actual (4), por lo que se llena en el contenedor (4).
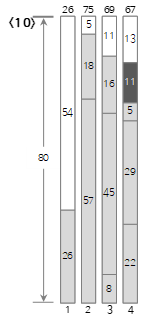
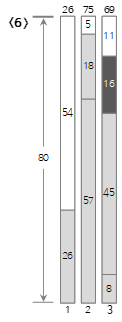
El décimo valor de entrada <11> es más pequeño que el tamaño restante (24) del contenedor actual (4), por lo que se llena en el contenedor (4).
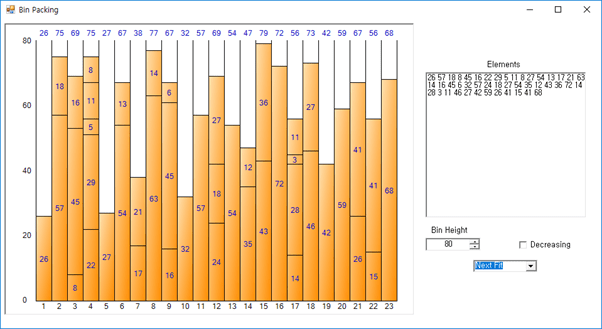
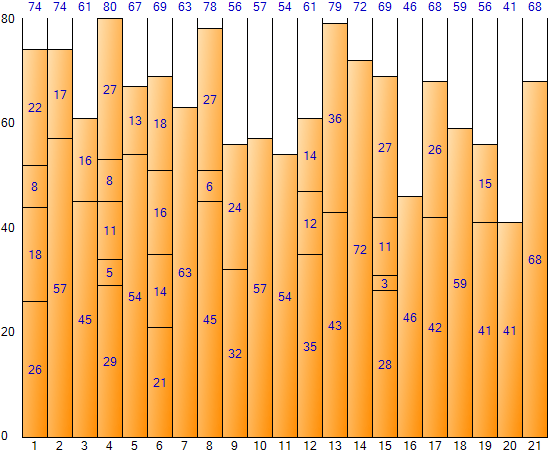
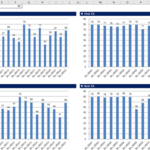
Si continúa llenando hasta el último elemento en el método Next Fit, puede obtener el siguiente resultado. (Pantalla de resultados de la aplicación de muestra de embalaje de contenedores)
Como se puede ver en la figura anterior, el resultado del método Next Fit es difícil de ver como el resultado óptimo debido a la gran pérdida de espacio. Sin embargo, tiene la ventaja de una rápida velocidad de ejecución debido al pequeño número de iteraciones. El espacio total es 1.840 (tamaño 80 por contenedor * número de contenedores 23), el espacio restante total es 488 y la ineficiencia de espacio es de aproximadamente 26.52% (488/1.840).
2.3. Algoritmo de primer ajuste
Para cada artículo, verifique si se puede llenar todo el contenedor, llénelo en el primer contenedor que se pueda llenar y, si no, cree un contenedor nuevo y llénelo.
// Pseudo code
item(1)을 새로운 Bin(1)에 채운다.
for (i=2; i<=item 개수; i++) {
for (j=1; j<=Bin갯수: j++) { // 항상 처음 Bin부터
if (item(i).Size <= Bin(j).남은공간Size) {
// item(i)를 채울 수 있는 Bin(j) 탐색
Bin(j)에 item(i)를 채운다;
exit for;
}
}
if (마지막 Bin까지 탐색해도 채울 수 없었으면) {
새로운 Bin(j+1)을 생성하고 item(i)를 채운다;
}
}
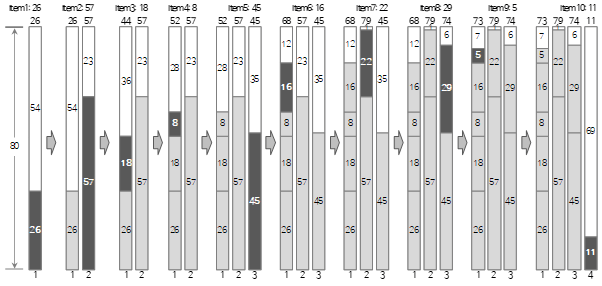
El proceso de llenar hasta los primeros 10 de los datos de entrada anteriores con el método First Fit se muestra en la siguiente figura.
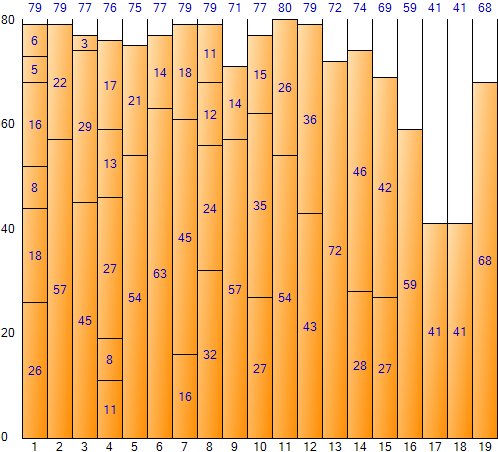
Rellenar todos los datos de entrada de esta manera da el siguiente resultado: (Pantalla de resultados de la aplicación de muestra de embalaje de contenedores)
El método First Fit tiene la ventaja de que se desperdicia menos espacio que Next Fit y el espacio total es más pequeño debido a la menor cantidad de contenedores. Sin embargo, la desventaja es que el tiempo de ejecución es largo debido al número relativamente grande de iteraciones. El espacio total es 1520 (tamaño 80 por contenedor * número de contenedores 19), el espacio restante total es 168 y la ineficiencia de espacio es de aproximadamente 11,051 TP2T (168/1520).
2.4. Algoritmo de peor ajuste
Para cada artículo, llene el contenedor que se puede llenar con el tamaño restante más grande entre todos los contenedores y, si no hay un contenedor adecuado, se crea y llena un contenedor nuevo.
// Pseudo code
item(1)을 새로운 Bin(1)에 채운다;
for (i=2; i<=item갯수; i++) {
long lMaxRemainSize = 0;
long lMaxRemainSizeBinIndex = 0;
for (j=1; j<=Bin갯수: j++) {
// 남은공간Size가 가장 큰 Bin 탐색
if (lMaxRemainSize < Bin(j).남은공간Size) {
lMaxRemainSize = Bin(j).남은공간Size;
lMaxRemainSizeBinIndex = j;
}
}
if (item(i).Size <= Bin(lMaxRemainSizeBinIndex) {
// 남은공간Size가 가장 큰 Bin에 item(i)를 채울 수 있는 경우
Bin(lMaxRemainSizeBinIndex)에 item(i)을 채운다;
}
else {
새로운 Bin(j+1)을 생성하고 item(i)을 채운다;
}
}
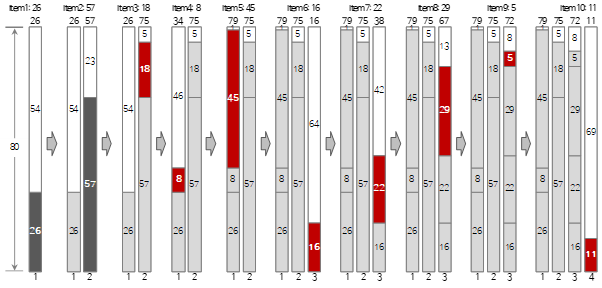
El proceso de llenar hasta los primeros 10 de los datos de entrada anteriores por el método de peor ajuste se muestra en la figura a continuación.
En la figura, el elemento rojo indica un caso en el que el método de llenado es diferente del método de primer ajuste.
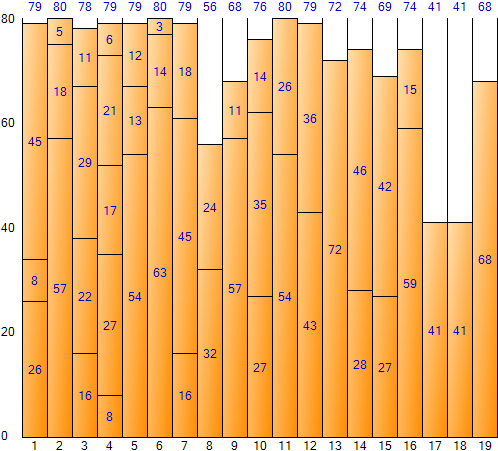
Rellenar todos los datos de entrada de esta manera da el siguiente resultado: (Pantalla de resultados de la aplicación de muestra de embalaje de contenedores)
El método Worst Fit desperdicia menos espacio que Next Fit, pero desperdicia más espacio que First Fit. El espacio total es 1680 (tamaño 80 por contenedor * número de contenedores 21), el espacio restante total es 328 y la ineficiencia de espacio es de aproximadamente 19,521 TP2T (328/1680).
2.5. Algoritmo de mejor ajuste
Para cada artículo, es un método para encontrar y llenar un contenedor que tenga el tamaño restante más pequeño entre todos los contenedores y pueda llenar el artículo correspondiente, y si no hay un contenedor adecuado, se crea y llena un nuevo contenedor.
// Pseudo code
for (i=2; i<=item갯수; i++) {
long lMinRemainSize = 제약조건으로 입력한 Bin의 최대 크기;
long lMinRemainSizeBinIndex = 0;
for (j=1; j<=Bin갯수: j++) {
// 남은공간Size가 가장 적으면서 item(i).Size를 채울 수 있는 Bin 탐색
if (oBin(j).남은공간Size >= item(i).SIze) and
(lMinRemainSize > oBin(j).남은공간Size)
lMinRemainSize = Bin(j).남은공간Size;
lMinRemainSizeBinIndex = j;
}
}
if (적합한 Bin을 찾았으면) {
Bin(lMinRemainSizeBinIndex)에 item(i)을 채운다;
}
else {
새로운 Bin(j+1)을 생성하고 item(i)을 채운다;
}
}
El proceso de llenar hasta los primeros 10 de los datos de entrada anteriores en el método Best Fit se muestra en la siguiente figura.
En la figura, el elemento rojo indica un caso en el que el método de llenado es diferente del método de primer ajuste. La comparación del proceso con First Fit y Worst Fit brinda una comprensión clara del método.
Rellenar todos los datos de entrada de esta manera da el siguiente resultado: (Pantalla de resultados de la aplicación de muestra de embalaje de contenedores)
El método de mejor ajuste generalmente logra los resultados más óptimos, pero tiene la desventaja de que lleva mucho tiempo ejecutarlo debido a la gran cantidad de iteraciones. El espacio total es 1520 (tamaño 80 por contenedor * número de contenedores 19), el espacio restante total es 168 y la ineficiencia de espacio es de aproximadamente 11,051 TP2T (168/1520).
El resultado de los métodos First Fit y Best Fit que tienen la misma cantidad de contenedores y el mismo espacio residual es exclusivo de los datos de entrada utilizados como ejemplo y es posible que no siempre sea el mismo.
Hemos analizado cada algoritmo hasta ahora y, a continuación, compararemos el método de aplicar la ordenación descendente y el resultado de la aplicación de cada algoritmo.
<< Lista de artículos relacionados >>
- Optimización de la distribución del trabajo utilizando un algoritmo de empaque de contenedores unidimensional_1.Descripción general
- Optimización de la distribución del trabajo mediante bin packing algorítmico unidimensional_2.Algoritmo (1)
- Optimización de la distribución del trabajo utilizando bin packing unidimensional algoritmo_2.Algoritmo(2)
- Optimización de la distribución del trabajo mediante el algoritmo bin packing unidimensional_3.Implementación (1)
- Optimización de la distribución del trabajo mediante el algoritmo bin packing unidimensional_3.Implementación (2)
- Optimización de la distribución del trabajo utilizando un algoritmo de empaque de contenedores unidimensional_4.Adjunto
- Cambios recientes de la herramienta de embalaje de contenedores unidimensionales (al 21 de marzo de 2021)
- Herramienta de optimización de la distribución del trabajo utilizando un algoritmo de empaque de contenedores unidimensional. Contenido completo, Descargar