Optimización de la distribución del trabajo utilizando un algoritmo de empaque de contenedores unidimensional_1.Descripción general
En este artículo, veremos el concepto y el algoritmo del empaque de contenedores unidimensional y descubriremos cómo optimizarlo con el objetivo de la cantidad mínima de grupos de trabajo y el tiempo de ejecución mínimo al usarlo. Además, presentaré la herramienta Bin Packing unidimensional que implementé directamente con Excel VBA y analizaré el caso del uso del paquete provisto en Python.
El código fuente de la herramienta implementada en Excel VBA y los ejemplos implementados en Python se pueden encontrar en el siguiente enlace.
Enlace: https://github.com/DAToolset/1D-bin-packing
1. Descripción general del algoritmo de optimización de embalaje de contenedores unidimensionales
1.1. La necesidad de empacar en contenedores
Considere el siguiente caso.
Caso 1)
Es un entorno con servidores de base de datos A y B. A es un servidor que gestiona unas 3.000 mesas y se está ejecutando actualmente, y B es un servidor recién creado y vacío. El servidor A tiene un total de 6 TB de datos. Queremos extraer los datos de la tabla de destino del servidor A dentro de un tiempo limitado (por ejemplo, 6 horas) y entregarlos al servidor B. Para completar la extracción de datos lo más rápido posible, ¿en cuántos grupos se deben dividir las tablas y qué tablas se deben colocar en cada grupo para lograr el resultado deseado? Esta tarea debe ejecutarse periódicamente, al menos una vez al mes. Se puede agregar una nueva tabla al servidor A para cada ejecución, y la cantidad de datos en cada tabla se puede aumentar o disminuir.
Caso 2)
Hay alrededor de 5.000 trabajos (procedimiento o SQL, etc.). Suponiendo que no hay orden ni dependencia de cada trabajo, para minimizar el tiempo de ejecución general, ¿en cuántos grupos se deben dividir los trabajos y qué trabajos se deben colocar en qué grupo?
Como en el caso anterior, encontrar la combinación óptima de cientos o miles de elementos requiere una cantidad significativa de tiempo y esfuerzo por parte de una persona que lo intente manualmente. Incluso si encuentra manualmente una combinación de grupos de tareas, no es sencillo verificar que la combinación sea óptima.
La razón por la que se necesita el algoritmo Bin Packing es por razones económicas que producen el máximo efecto con la mínima inversión. El algoritmo de empaque de contenedores se puede usar universalmente cuando es necesario encontrar la combinación óptima que se pueda llenar tanto como sea posible dentro de un tiempo limitado o dentro de un espacio limitado.
1.2. Concepto de embalaje de contenedores
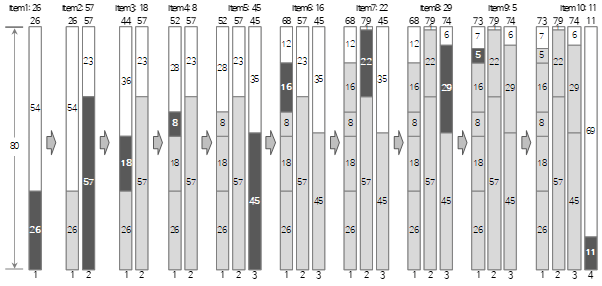
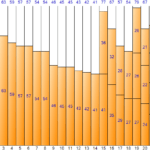
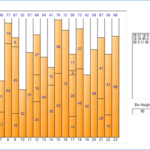
Bin Packing es un algoritmo de optimización que averigua cuántos contenedores se necesitan para llenar un contenedor con tantos elementos como sea posible. Hay dos valores de entrada. El primero es el tamaño de un contenedor y el segundo es una lista de elementos. La lista de artículos consta de un nombre y un tamaño, y el nombre se ingresa opcionalmente. El valor de salida es el número de contenedores optimizados (menos) y una lista de elementos que se incluirán en cada contenedor.
En el caso 1 del ejemplo anterior, la cantidad de bytes de la tabla, la cantidad de filas o el tiempo promedio que se tarda en extraer los datos de cada tabla cuando se ejecuta varias veces se puede ver como el tamaño. El tiempo de cada trabajo se puede ver como el tamaño.
Echemos un vistazo más de cerca al significado de "minimizar el tiempo total de ejecución" en el Caso 2. El tiempo de ejecución total es el mismo que el tiempo de ejecución más largo entre los tiempos de ejecución del grupo de trabajo en el que se ubica cada trabajo.
Es decir, el tiempo de ejecución total = Max (Tiempo de ejecución individual del grupo de trabajo). En otras palabras, dado que el tiempo de ejecución general se puede minimizar cuando la diferencia en el tiempo de ejecución de cada grupo de trabajo es pequeña, "minimizar el tiempo de ejecución general" es lo mismo que "hacer que el tiempo de ejecución individual de cada grupo de trabajo sea casi igual". ”.
Cuando el tamaño de un contenedor y el tamaño de un artículo se pueden expresar en un número cuantitativo, como la longitud y el tiempo, se puede aplicar el empaque de contenedores unidimensional. El empaque de contenedores unidimensional es un algoritmo que recibe elementos de varios tamaños y utiliza el tamaño máximo de un contenedor como una restricción para obtener una lista de resultados al organizar cada elemento de acuerdo con la restricción. Los conceptos de entrada, restricción y salida se resumen a continuación.
- Entrada: una lista del nombre y el tamaño de cada elemento
- Restricción: tamaño máximo de un contenedor
- Salida: el número de contenedores necesarios, una lista de los elementos que contiene cada contenedor
Se aplica el embalaje de contenedores de 2 dimensiones cuando el tamaño se puede expresar en dos números (ancho, alto) y el embalaje de contenedores de 3 dimensiones cuando se puede expresar en tres números (ancho, alto, alto). El embalaje de contenedores 2D se puede aplicar al organizar o cortar formas para minimizar el espacio vacío en un plano 2D. El embalaje de contenedores 3D se puede aplicar cuando desea apilar elementos en un espacio 3D con menos espacio vacío. Un caso típico en el que se puede aplicar el embalaje en contenedores tridimensionales es la optimización del espacio en el que se minimiza el espacio restante al cargar cajas en un vehículo de reparto. El embalaje en contenedores 2 y 3D no está cubierto en este artículo.
Veremos más detalles en el siguiente artículo.
<< Lista de artículos relacionados >>
- Optimización de la distribución del trabajo utilizando un algoritmo de empaque de contenedores unidimensional_1.Descripción general
- Optimización de la distribución del trabajo mediante bin packing algorítmico unidimensional_2.Algoritmo (1)
- Optimización de la distribución del trabajo utilizando bin packing unidimensional algoritmo_2.Algoritmo(2)
- Optimización de la distribución del trabajo mediante el algoritmo bin packing unidimensional_3.Implementación (1)
- Optimización de la distribución del trabajo mediante el algoritmo bin packing unidimensional_3.Implementación (2)
- Optimización de la distribución del trabajo utilizando un algoritmo de empaque de contenedores unidimensional_4.Adjunto
- Cambios recientes de la herramienta de embalaje de contenedores unidimensionales (al 21 de marzo de 2021)
- Herramienta de optimización de la distribución del trabajo utilizando un algoritmo de empaque de contenedores unidimensional. Contenido completo, Descargar