Optimización de la distribución del trabajo utilizando bin packing unidimensional algoritmo_2.Algoritmo(2)

2.6. Aplicar clasificación descendente por tamaño del artículo

Hasta ahora, se han revisado el método de operación y los resultados de ejecución de cada algoritmo de Next Fit, First Fit, Worst Fit y Best Fit. Cuando el tamaño de los datos de entrada se procesa en un orden aleatorio cuando el tamaño de los datos de entrada no está dispuesto en un cierto orden, el resultado es diferente cuando se procesa en el estado ordenado. Rellenar primero los elementos grandes generalmente produce buenos resultados, por lo que puede pensar en clasificarlos en orden descendente por el tamaño de los elementos y procesarlos primero.

Primero, los datos de entrada y los datos ordenados en orden descendente son los siguientes.

Datos de entrada # 26 57 18 8 45 16 22 29 5 11 8 27 54 13 17 21 63 14 16 45 6 32 57 24 18 27 54 35 12 43 36 72 14 28 3 11 46 27 42 4 1 6 826 4 1 6 826

# Datos de entrada de clasificación descendente 72 68 63 59 57 57 54 54 46 45 45 43 42 41 41 36 35 32 29 28 27 27 27 26 26 24 22 21 18 18 17 16 16 15 14 14 1 3 6 1 8 5

Veamos los resultados de ejecutar cada algoritmo con los datos ordenados en orden descendente como entrada.

2.7. Siguiente Ajustar con clasificación descendente

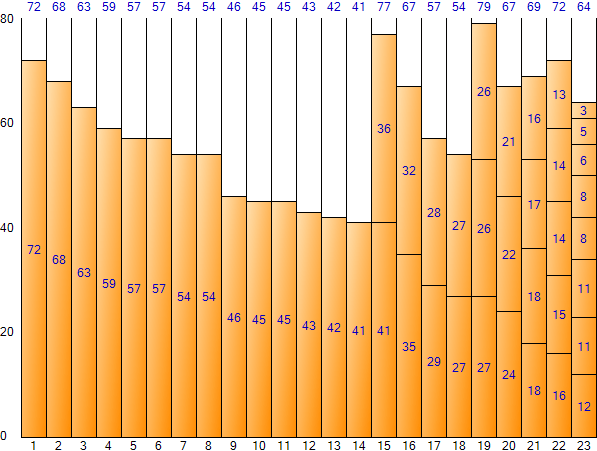
El espacio total es 1.840 (tamaño 80 por contenedor * número de contenedores 23), el espacio restante total es 488 y la ineficiencia de espacio es de aproximadamente 26.52% (488/1.840).

2.8. Primer ajuste con clasificación descendente

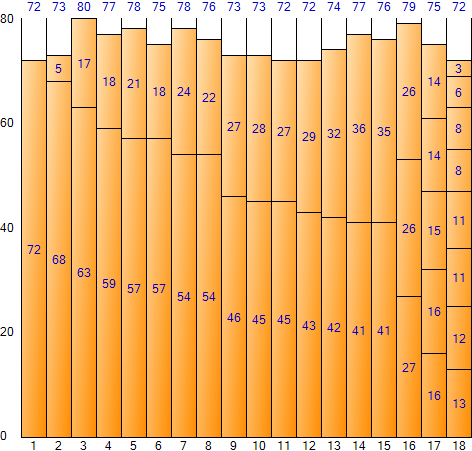
El espacio total es 1440 (tamaño 80 por contenedor * número de contenedores 18), el espacio restante total es 88 y la ineficiencia de espacio es de aproximadamente 6,111 TP2T (88/1440).

2.9. Peor ajuste con orden descendente

El espacio total es 1440 (tamaño 80 por contenedor * número de contenedores 18), el espacio restante total es 88 y la ineficiencia de espacio es de aproximadamente 6,111 TP2T (88/1440).

2.10. Ajuste óptimo con clasificación descendente

El espacio total es 1440 (tamaño 80 por contenedor * número de contenedores 18), el espacio restante total es 88 y la ineficiencia de espacio es de aproximadamente 6,111 TP2T (88/1440).

2.11. Comparación de los resultados de la aplicación del algoritmo

 En el caso revisado anteriormente, a excepción de Next Fit, que tiene la mayor ineficiencia, la suma espacial residual y la ineficiencia espacial de First Fit, Worst Fit y Best Fit arrojaron los mismos resultados, y los elementos llenados en cada contenedor se configuraron de manera diferente. .

Tenga en cuenta que el mismo resultado es una coincidencia basada en los datos de entrada y las restricciones en este caso. Si los datos de entrada y las restricciones son diferentes, la suma espacial residual, la ineficiencia espacial y la lista de contenedores de composición de artículos pueden ser diferentes.

La comparación del resultado no ordenado con el resultado ordenado es la siguiente.

▼ Siguiente ajuste

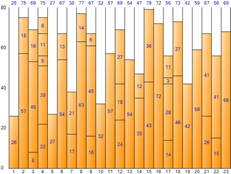
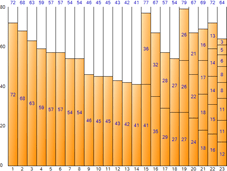
▼ Primer ajuste

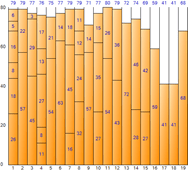
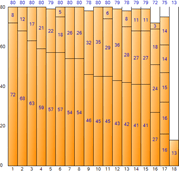
▼ Peor ajuste

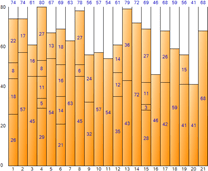
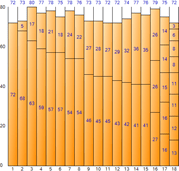
▼ Mejor ajuste

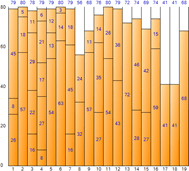
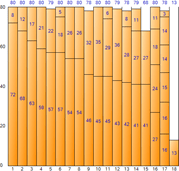
A continuación se muestra la información cuantitativa que produce la ejecución de cada algoritmo.

algoritmo	Artículo	antes de clasificar	después de clasificar	comparar
Siguiente ajuste	número de comparaciones	44	44	ningún cambio
	todo el espacio	1,840	1,840
	Espacio restante total	488	488
	ineficiencia espacial	26.525	26.525
primer ajuste	número de comparaciones	330	448	El número de comparaciones aumentó, pero la ineficiencia del espacio disminuyó y mejoró
	todo el espacio	1,520	1,440
	Espacio restante total	168	88
	ineficiencia espacial	11.05%	6.11%
peor ajuste	número de comparaciones	465	643
	todo el espacio	1,680	1,440
	Espacio restante total	328	88
	ineficiencia espacial	19.52%	6.11%
Mejor ajuste	número de comparaciones	428	643
	todo el espacio	1,520	1,440
	Espacio restante total	168	88
	ineficiencia espacial	11.05%	6.11%

En la tabla anterior, el número de comparaciones se mide aproximadamente con la herramienta basada en Excel VBA que se presentará a continuación. Si observa lo anterior, puede ver que el resultado de ejecutar Bin Packing después de clasificar en orden descendente por tamaño de artículo reduce la ineficiencia del espacio y se llena más densamente. Se puede ver que ordenar primero y aplicar el algoritmo puede obtener resultados más optimizados.

Best Fit no siempre es óptimo. Es conveniente revisar los resultados de ejecución de cada algoritmo y seleccionar el resultado óptimo para cada situación.

---

Hasta ahora, hemos analizado en detalle el algoritmo Bin Packing. A continuación, veremos las herramientas que implementan este algoritmo.

---

<< Lista de artículos relacionados >>

• Optimización de la distribución del trabajo utilizando un algoritmo de empaque de contenedores unidimensional_1.Descripción general
• Optimización de la distribución del trabajo mediante bin packing algorítmico unidimensional_2.Algoritmo (1)
• Optimización de la distribución del trabajo utilizando bin packing unidimensional algoritmo_2.Algoritmo(2)
• Optimización de la distribución del trabajo mediante el algoritmo bin packing unidimensional_3.Implementación (1)
• Optimización de la distribución del trabajo mediante el algoritmo bin packing unidimensional_3.Implementación (2)
• Optimización de la distribución del trabajo utilizando un algoritmo de empaque de contenedores unidimensional_4.Adjunto
• Cambios recientes de la herramienta de embalaje de contenedores unidimensionales (al 21 de marzo de 2021)
• Herramienta de optimización de la distribución del trabajo utilizando un algoritmo de empaque de contenedores unidimensional. Contenido completo, Descargar