Optimierung der Arbeitsverteilung durch eindimensionalen Bin-Packing-Algorithmus_3.Implementierung (2)

3.2. Nutzen Sie das Python Bin Packing-Paket

3.2.1. Einführung und Installation des Pakets Python Bin Packing

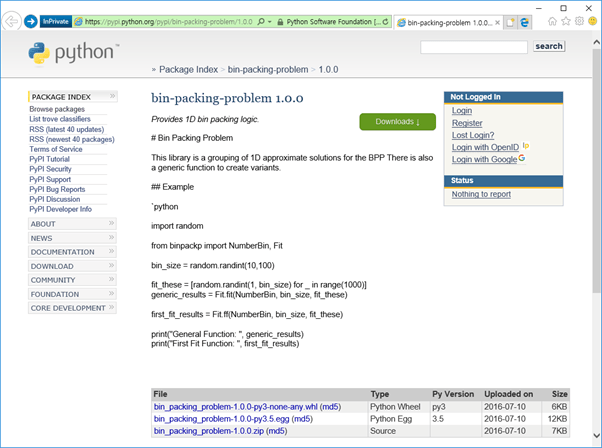
Bin Packing-Pakete, die in Python verfügbar sind, sind auf der Pypi-Webseite (Python Package Index) aufgelistet. https://pypi.python.org/pypi/bin-packing-problem/1.0.0 zur Verfügung gestellt von Von dieser URL aus können Sie auf die kurze Beschreibung und den Beispielquellcode des Bin Packing-Pakets verweisen und die Paketdatei herunterladen, um den implementierten Quellcode zu überprüfen.

Die Methode, die das folgende Bin-Packing implementiert, wird im Fit-Modul dieses Pakets bereitgestellt.

Algorithmus	Methode (keine Sortierung angewendet)	Methode (Sortierung anwenden)
Nächste Passform	nf	– (in v1.0 nicht implementiert)
Erster Fit	ff	ffd
Schlechteste Passform	wf	wfd
Beste Passform	bf	bfd

Die Installation verwendet pip, den Python-Paketmanager, wie folgt.

pip install bin-packing-problem

3.2.2. Beispiel-Quellcode für Behälterverpackung

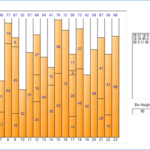
Im Folgenden finden Sie einen Beispielquellcode, der das oben installierte Bin Packing-Paket verwendet. Es wurden die gleichen Eingabewerte verwendet, die in der Beschreibung des Bin-Packing-Algorithmus in Tabelle 2 verwendet wurden.

Als Referenz weiß ich nicht, ob es die Absicht des Paketentwicklers oder ein Fehler ist, aber die Methode nfd (nächste Anpassung absteigend) ist nicht implementiert und auskommentiert.

from binpackp import NumberBin, Fit

def print_result(fit_name, fit_result):
    print(fit_name + " Result: ", fit_result)
    for bin in fit_result.bins:
        print(bin)
    print()

bin_size = 80
fit_these = [26, 57, 18, 8, 45, 16, 22, 29, 5, 11, 8, 27, 54, 13, 17, 21, 63, 14, 16, 45, 6, 32, 57, 24, 18, 27, 54, 35, 12, 43, 36, 72, 14, 28, 3, 11, 46, 27, 42, 59, 26, 41, 15, 41, 68]

next_fit_results = Fit.nf(NumberBin, bin_size, fit_these)
first_fit_results = Fit.ff(NumberBin, bin_size, fit_these)
worst_fit_result = Fit.wf(NumberBin, bin_size, fit_these)
best_fit_result = Fit.bf(NumberBin, bin_size, fit_these)

# sorted_next_fit_results = Fit.nfd(NumberBin, bin_size, fit_these) # not implemented
sorted_first_fit_results = Fit.ffd(NumberBin, bin_size, fit_these)
sorted_worst_fit_result = Fit.wfd(NumberBin, bin_size, fit_these)
sorted_best_fit_result = Fit.bfd(NumberBin, bin_size, fit_these)

print_result("Next Fit", next_fit_results)
print_result("First Fit", first_fit_results)
print_result("Worst Fit", worst_fit_result)
print_result("Best Fit", best_fit_result)

# print_result("Next Fit With Sort", next_fit_results) # not implemented
print_result("First Fit With Sort", sorted_first_fit_results)
print_result("Worst Fit With Sort", sorted_worst_fit_result)
print_result("Best Fit With Sort", sorted_best_fit_result)

3.2.3. Bin Packing-Beispielquellcodeausgabe

Das Ergebnis der Ausführung des Beispielquellcodes ist wie folgt. Obwohl das Ausführungsergebnis und die Ausgabereihenfolge jedes in Tabelle 2 beschriebenen Algorithmus unterschiedlich sind, ist ersichtlich, dass die gefüllten Inhalte dieselben sind.

Next Fit Result:  <BPResult (Total Bins: 23, Total Volume: 1840, Unused Volume: 488)>
<NumberBin>(Volume: 26/80, Items: [26])
<NumberBin>(Volume: 75/80, Items: [57, 18])
<NumberBin>(Volume: 69/80, Items: [8, 45, 16])
<NumberBin>(Volume: 75/80, Items: [22, 29, 5, 11, 8])
<NumberBin>(Volume: 27/80, Items: [27])
<NumberBin>(Volume: 67/80, Items: [54, 13])
<NumberBin>(Volume: 38/80, Items: [17, 21])
<NumberBin>(Volume: 77/80, Items: [63, 14])
<NumberBin>(Volume: 67/80, Items: [16, 45, 6])
<NumberBin>(Volume: 32/80, Items: [32])
<NumberBin>(Volume: 57/80, Items: [57])
<NumberBin>(Volume: 69/80, Items: [24, 18, 27])
<NumberBin>(Volume: 54/80, Items: [54])
<NumberBin>(Volume: 47/80, Items: [35, 12])
<NumberBin>(Volume: 79/80, Items: [43, 36])
<NumberBin>(Volume: 72/80, Items: [72])
<NumberBin>(Volume: 56/80, Items: [14, 28, 3, 11])
<NumberBin>(Volume: 73/80, Items: [46, 27])
<NumberBin>(Volume: 42/80, Items: [42])
<NumberBin>(Volume: 59/80, Items: [59])
<NumberBin>(Volume: 67/80, Items: [26, 41])
<NumberBin>(Volume: 56/80, Items: [15, 41])
<NumberBin>(Volume: 68/80, Items: [68])

First Fit Result:  <BPResult (Total Bins: 19, Total Volume: 1520, Unused Volume: 168)>
<NumberBin>(Volume: 80/80, Items: [54, 26])
<NumberBin>(Volume: 79/80, Items: [26, 18, 8, 16, 5, 6])
<NumberBin>(Volume: 79/80, Items: [57, 22])
<NumberBin>(Volume: 77/80, Items: [45, 29, 3])
<NumberBin>(Volume: 76/80, Items: [11, 8, 27, 13, 17])
<NumberBin>(Volume: 75/80, Items: [54, 21])
<NumberBin>(Volume: 77/80, Items: [63, 14])
<NumberBin>(Volume: 79/80, Items: [16, 45, 18])
<NumberBin>(Volume: 79/80, Items: [32, 24, 12, 11])
<NumberBin>(Volume: 71/80, Items: [57, 14])
<NumberBin>(Volume: 77/80, Items: [27, 35, 15])
<NumberBin>(Volume: 79/80, Items: [43, 36])
<NumberBin>(Volume: 72/80, Items: [72])
<NumberBin>(Volume: 74/80, Items: [28, 46])
<NumberBin>(Volume: 69/80, Items: [27, 42])
<NumberBin>(Volume: 59/80, Items: [59])
<NumberBin>(Volume: 41/80, Items: [41])
<NumberBin>(Volume: 41/80, Items: [41])
<NumberBin>(Volume: 68/80, Items: [68])

Worst Fit Result:  <BPResult (Total Bins: 21, Total Volume: 1680, Unused Volume: 328)>
<NumberBin>(Volume: 80/80, Items: [29, 5, 11, 8, 27])
<NumberBin>(Volume: 41/80, Items: [41])
<NumberBin>(Volume: 46/80, Items: [46])
<NumberBin>(Volume: 54/80, Items: [54])
<NumberBin>(Volume: 56/80, Items: [41, 15])
<NumberBin>(Volume: 56/80, Items: [32, 24])
<NumberBin>(Volume: 57/80, Items: [57])
<NumberBin>(Volume: 59/80, Items: [59])
<NumberBin>(Volume: 61/80, Items: [35, 12, 14])
<NumberBin>(Volume: 61/80, Items: [45, 16])
<NumberBin>(Volume: 63/80, Items: [63])
<NumberBin>(Volume: 67/80, Items: [54, 13])
<NumberBin>(Volume: 68/80, Items: [42, 26])
<NumberBin>(Volume: 68/80, Items: [68])
<NumberBin>(Volume: 69/80, Items: [28, 3, 11, 27])
<NumberBin>(Volume: 69/80, Items: [45, 6, 18])
<NumberBin>(Volume: 72/80, Items: [72])
<NumberBin>(Volume: 74/80, Items: [57, 17])
<NumberBin>(Volume: 74/80, Items: [26, 18, 8, 22])
<NumberBin>(Volume: 78/80, Items: [21, 14, 16, 27])
<NumberBin>(Volume: 79/80, Items: [43, 36])

Best Fit Result:  <BPResult (Total Bins: 19, Total Volume: 1520, Unused Volume: 168)>
<NumberBin>(Volume: 80/80, Items: [57, 18, 5])
<NumberBin>(Volume: 80/80, Items: [63, 14, 3])
<NumberBin>(Volume: 80/80, Items: [54, 26])
<NumberBin>(Volume: 79/80, Items: [26, 8, 45])
<NumberBin>(Volume: 79/80, Items: [8, 27, 17, 21, 6])
<NumberBin>(Volume: 79/80, Items: [16, 45, 18])
<NumberBin>(Volume: 79/80, Items: [54, 13, 12])
<NumberBin>(Volume: 79/80, Items: [43, 36])
<NumberBin>(Volume: 78/80, Items: [16, 22, 29, 11])
<NumberBin>(Volume: 76/80, Items: [27, 35, 14])
<NumberBin>(Volume: 74/80, Items: [28, 46])
<NumberBin>(Volume: 74/80, Items: [59, 15])
<NumberBin>(Volume: 72/80, Items: [72])
<NumberBin>(Volume: 69/80, Items: [27, 42])
<NumberBin>(Volume: 68/80, Items: [57, 11])
<NumberBin>(Volume: 68/80, Items: [68])
<NumberBin>(Volume: 56/80, Items: [32, 24])
<NumberBin>(Volume: 41/80, Items: [41])
<NumberBin>(Volume: 41/80, Items: [41])

First Fit With Sort Result:  <BPResult (Total Bins: 18, Total Volume: 1440, Unused Volume: 88)>
<NumberBin>(Volume: 80/80, Items: [45, 35])
<NumberBin>(Volume: 80/80, Items: [54, 26])
<NumberBin>(Volume: 80/80, Items: [54, 26])
<NumberBin>(Volume: 80/80, Items: [59, 21])
<NumberBin>(Volume: 80/80, Items: [63, 17])
<NumberBin>(Volume: 80/80, Items: [68, 12])
<NumberBin>(Volume: 80/80, Items: [72, 8])
<NumberBin>(Volume: 80/80, Items: [45, 29, 6])
<NumberBin>(Volume: 80/80, Items: [57, 18, 5])
<NumberBin>(Volume: 79/80, Items: [57, 22])
<NumberBin>(Volume: 78/80, Items: [46, 32])
<NumberBin>(Volume: 79/80, Items: [43, 36])
<NumberBin>(Volume: 78/80, Items: [42, 28, 8])
<NumberBin>(Volume: 79/80, Items: [41, 27, 11])
<NumberBin>(Volume: 79/80, Items: [41, 27, 11])
<NumberBin>(Volume: 72/80, Items: [27, 24, 18, 3])
<NumberBin>(Volume: 75/80, Items: [16, 16, 15, 14, 14])
<NumberBin>(Volume: 13/80, Items: [13])

Worst Fit With Sort Result:  <BPResult (Total Bins: 18, Total Volume: 1440, Unused Volume: 88)>
<NumberBin>(Volume: 80/80, Items: [63, 17])
<NumberBin>(Volume: 72/80, Items: [13, 12, 11, 11, 8, 8, ...])
<NumberBin>(Volume: 72/80, Items: [45, 27])
<NumberBin>(Volume: 72/80, Items: [43, 29])
<NumberBin>(Volume: 72/80, Items: [72])
<NumberBin>(Volume: 73/80, Items: [68, 5])
<NumberBin>(Volume: 73/80, Items: [46, 27])
<NumberBin>(Volume: 73/80, Items: [45, 28])
<NumberBin>(Volume: 74/80, Items: [42, 32])
<NumberBin>(Volume: 75/80, Items: [16, 16, 15, 14, 14])
<NumberBin>(Volume: 75/80, Items: [57, 18])
<NumberBin>(Volume: 76/80, Items: [54, 22])
<NumberBin>(Volume: 76/80, Items: [41, 35])
<NumberBin>(Volume: 77/80, Items: [59, 18])
<NumberBin>(Volume: 77/80, Items: [41, 36])
<NumberBin>(Volume: 78/80, Items: [57, 21])
<NumberBin>(Volume: 78/80, Items: [54, 24])
<NumberBin>(Volume: 79/80, Items: [27, 26, 26])

Best Fit With Sort Result:  <BPResult (Total Bins: 18, Total Volume: 1440, Unused Volume: 88)>
<NumberBin>(Volume: 80/80, Items: [45, 35])
<NumberBin>(Volume: 80/80, Items: [54, 26])
<NumberBin>(Volume: 80/80, Items: [54, 26])
<NumberBin>(Volume: 80/80, Items: [59, 21])
<NumberBin>(Volume: 80/80, Items: [63, 17])
<NumberBin>(Volume: 80/80, Items: [68, 12])
<NumberBin>(Volume: 80/80, Items: [27, 24, 18, 11])
<NumberBin>(Volume: 80/80, Items: [72, 8])
<NumberBin>(Volume: 80/80, Items: [45, 29, 6])
<NumberBin>(Volume: 80/80, Items: [57, 18, 5])
<NumberBin>(Volume: 79/80, Items: [43, 36])
<NumberBin>(Volume: 79/80, Items: [57, 22])
<NumberBin>(Volume: 79/80, Items: [41, 27, 11])
<NumberBin>(Volume: 78/80, Items: [46, 32])
<NumberBin>(Volume: 78/80, Items: [42, 28, 8])
<NumberBin>(Volume: 78/80, Items: [16, 16, 15, 14, 14, 3])
<NumberBin>(Volume: 68/80, Items: [41, 27])
<NumberBin>(Volume: 13/80, Items: [13])

4. Zukünftige Entwicklungsrichtung und Referenzmaterialien

Der bisher untersuchte Bin-Packing-Algorithmus setzt sich aus der Prämisse zusammen, dass jedes Item unabhängig und ohne Beziehung zueinander ist. Mit anderen Worten, es handelt sich um einen Algorithmus, der Abhängigkeiten nicht berücksichtigt, z. B. wenn Artikel zusammen in einen Behälter gefüllt werden müssen, weil zwischen Artikeln eine Vorrangbeziehung besteht.

Tatsächlich kann man sagen, dass es weit mehr Fälle gibt, in denen Abhängigkeiten bestehen, als Fälle, in denen keine Abhängigkeiten bestehen. Beispielsweise gibt es in der Praxis mehr Fälle, in denen Job2 und Job3 ausgeführt werden müssen, nachdem Job1 zuerst ausgeführt wurde, als den Fall, in dem Job1, Job2 und Job3 unabhängig voneinander ausgeführt werden können.

Es ist notwendig, den bisher bekannten Bin-Packing-Algorithmus weiterzuentwickeln, indem seine Abhängigkeiten reflektiert werden. In diesem Artikel haben wir uns nicht mit Bin Packing befasst, das Abhängigkeiten widerspiegelt. Ich wäre sehr dankbar, wenn jemand mitteilen könnte, was er durch weitere Forschung verbessert oder entwickelt hat.

Feedback zum Inhalt dieses Artikels ist ein Kommentar bzw https://github.com/DAToolset/1D-bin-packing Github-Problem, bitte senden Sie es an meine E-Mail.

---

<< Liste verwandter Artikel >>

• Optimierung der Arbeitsverteilung durch eindimensionalen Bin-Packing-Algorithmus_1.Überblick
• Optimierung der Arbeitsverteilung durch eindimensionalen Bin-Packing-Algorithmus_2.Algorithmus (1)
• Optimierung der Arbeitsverteilung mit eindimensionalem Bin-Packing-Algorithmus_2.Algorithmus(2)
• Optimierung der Arbeitsverteilung durch eindimensionalen Bin-Packing-Algorithmus_3.Implementierung (1)
• Optimierung der Arbeitsverteilung durch eindimensionalen Bin-Packing-Algorithmus_3.Implementierung (2)
• Optimierung der Arbeitsverteilung durch eindimensionalen Bin-Packing-Algorithmus_4.Attachment
• Letzte Änderungen am eindimensionalen Bin-Packing-Tool (Stand: 21. März 2021)
• Tool zur Optimierung der Arbeitsverteilung mit eindimensionalem Bin-Packing-Algorithmus Vollständiger Inhalt, Download