Optimierung der Arbeitsverteilung durch eindimensionalen Bin-Packing-Algorithmus_2.Algorithmus (1)
2. Eindimensionaler Bin-Packing-Algorithmus
2.1. Typ des eindimensionalen Bin-Packing-Algorithmus
Die vier repräsentativen Algorithmen von Bin Packing sind wie folgt.
- Next Fit: Füllen Sie den letzten Behälter oder den neuen Behälter aus
- First Fit: Suchen und befüllen Sie immer den ersten Behälter
- Am schlechtesten geeignet: Suchen und füllen Sie den Behälter, der den aktuellen Artikel mit der größten verbleibenden Größe unter allen Behältern füllen kann
- Best Fit: Suchen und füllen Sie den Behälter, der den aktuellen Artikel mit der kleinsten verbleibenden Größe unter allen Behältern füllen kann.
Darüber hinaus kann ein viel optimierteres Ergebnis erzielt werden, indem das gesamte Element in absteigender Reihenfolge der Größe sortiert und jeder Algorithmus angewendet wird. In Anbetracht der Methode zur Anwendung der absteigenden Sortierung kann gesagt werden, dass es insgesamt 8 Algorithmen gibt.
Die folgenden Eingaben und Beschränkungen werden zur Erläuterung verwendet. (Der Name des Artikels in der Eingabe entfällt und es wird nur die Größe beschrieben)
- Eingabe: 26 57 18 8 45 16 22 29 5 11 8 27 54 13 17 21 63 14 16 45 6 32 57 24 18 27 54 35 12 43 36 72 14 28 3 11 46 27 42 59 26 41 68
- Einschränkung: 80 (maximale Größe eines Behälters)
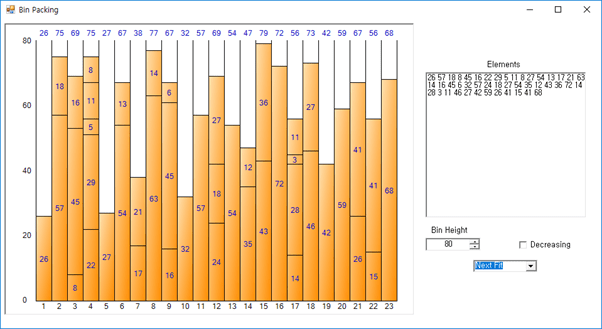
Hinweis: Dies sind Falldaten und Einschränkungen http://www.developerfusion.com/article/5540/bin-packing/ Die Grunddaten der Bin Packing Sample Application, die unter heruntergeladen werden kann. Der Bildschirm dieser Beispielanwendung sieht wie folgt aus.
Werfen wir einen detaillierten Blick auf den Pseudocode, den Verarbeitungsprozess und das Ausführungsergebnis jedes Algorithmus.
2.2. Next-Fit-Algorithmus
Für jeden Artikel wird der letzte Behälter gefüllt, wenn er gefüllt werden kann, und wenn er nicht gefüllt werden kann, wird ein neuer Behälter erstellt und gefüllt. Next Fit ist am einfachsten, aber das Ergebnis ist nicht optimal.
// Pseudo code
item(1)을 새로운 Bin(1)에 채운다.
for (i=2; i<=item 개수; i++) {
j = 마지막 Bin index
if (item(i).Size <= Bin(j).남은공간Size) {
Bin(j)에 item(i)를 채운다;
}
else {
새로운 Bin(j+1)을 생성하고 item(i)를 채운다;
}
}
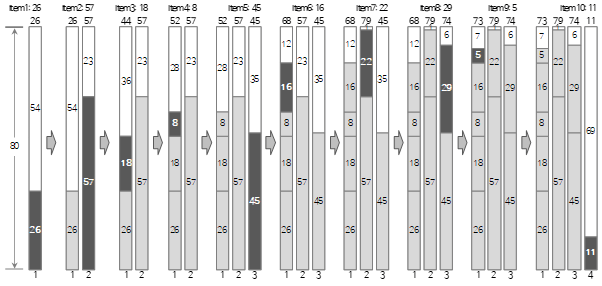
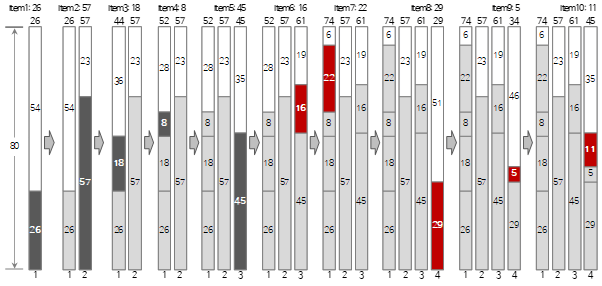
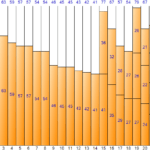
Schauen wir uns den Vorgang bis zur <10> der obigen Eingabewerte in der folgenden Abbildung an.
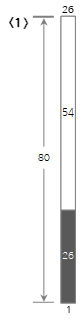
Der erste Eingabewert <26> erstellt ein neues Bin1 und füllt es.
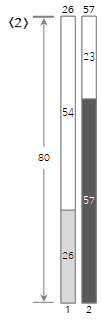
Da der zweite Eingabewert <57> größer als die verbleibende Größe (54) von Bin(1) ist und nicht gefüllt werden kann, wird ein neuer Bin(2) erstellt und gefüllt.
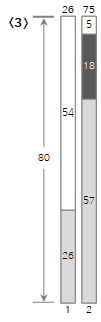
Der dritte Eingabewert <18> ist kleiner als die verbleibende Größe (23) des aktuellen Bin (2), also wird er in Bin (2) gefüllt.
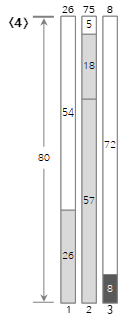
Da der vierte Eingabewert <8> größer als die verbleibende Größe (5) des aktuellen Bin (2) ist und nicht gefüllt werden kann, wird ein neuer Bin (3) erstellt und gefüllt. Wie Sie hier sehen können, verwendet die Next Fit-Methode nicht die bereits durchlaufenen Bins, auch wenn noch Platz vorhanden ist. Daher kann viel Platz verschwendet werden.
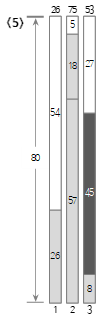
Der fünfte Eingabewert <45> ist kleiner als die verbleibende Größe (72) des aktuellen Bin (3), also wird er in Bin (3) gefüllt.
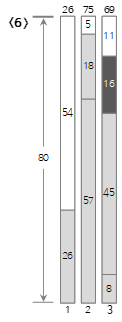
Der sechste Eingabewert <16> ist kleiner als die verbleibende Größe (27) des aktuellen Bin (3), also wird er in Bin (3) gefüllt.
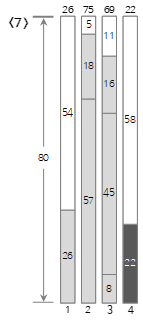
Da der siebte Eingabewert <22> größer als die verbleibende Größe von Bin(3) (11) ist und nicht gefüllt werden kann, wird ein neuer Bin(4) erstellt und gefüllt.
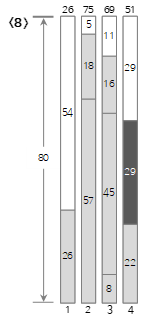
Der achte Eingabewert <29> ist kleiner als die verbleibende Größe (58) des aktuellen Bin (4), also wird er in Bin (4) gefüllt.
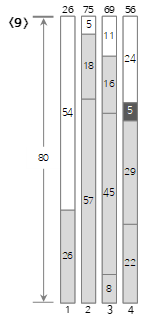
Der neunte Eingabewert <5> ist kleiner als die verbleibende Größe (29) des aktuellen Bin (4), also wird er in Bin (4) gefüllt.
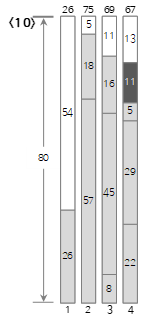
Der zehnte Eingabewert <11> ist kleiner als die verbleibende Größe (24) des aktuellen Bin (4), also wird er in Bin (4) gefüllt.
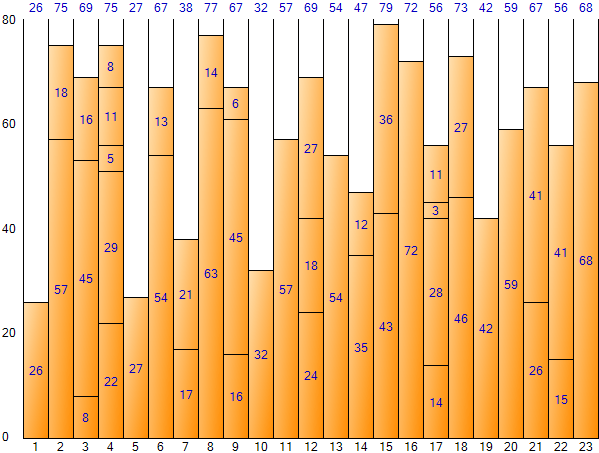
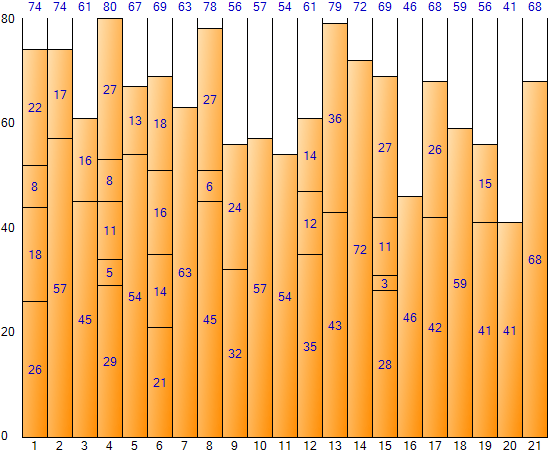
Wenn Sie bis zum letzten Element in der Next Fit-Methode auffüllen, können Sie das folgende Ergebnis erhalten. (Ergebnisbildschirm der Bin-Packing-Beispielanwendung)
Wie in der obigen Abbildung zu sehen ist, ist das Ergebnis der Next-Fit-Methode aufgrund der großen Platzverschwendung schwer als optimales Ergebnis zu sehen. Es hat jedoch den Vorteil einer schnellen Ausführungsgeschwindigkeit aufgrund der geringen Anzahl von Iterationen. Der Gesamtplatz beträgt 1.840 (Größe 80 pro Fach * Anzahl der Fächer 23), und der verbleibende Gesamtplatz beträgt 488, und die Platzineffizienz beträgt etwa 26,521 TP2T (488/1.840).
2.3. First-Fit-Algorithmus
Prüfen Sie für jeden Artikel, ob der gesamte Behälter gefüllt werden kann, füllen Sie ihn in den ersten Behälter, der gefüllt werden kann, und wenn nicht, erstellen Sie einen neuen Behälter und füllen Sie ihn.
// Pseudo code
item(1)을 새로운 Bin(1)에 채운다.
for (i=2; i<=item 개수; i++) {
for (j=1; j<=Bin갯수: j++) { // 항상 처음 Bin부터
if (item(i).Size <= Bin(j).남은공간Size) {
// item(i)를 채울 수 있는 Bin(j) 탐색
Bin(j)에 item(i)를 채운다;
exit for;
}
}
if (마지막 Bin까지 탐색해도 채울 수 없었으면) {
새로운 Bin(j+1)을 생성하고 item(i)를 채운다;
}
}
Der Vorgang des Auffüllens der ersten 10 der obigen Eingabedaten mit der First-Fit-Methode ist in der folgenden Abbildung dargestellt.
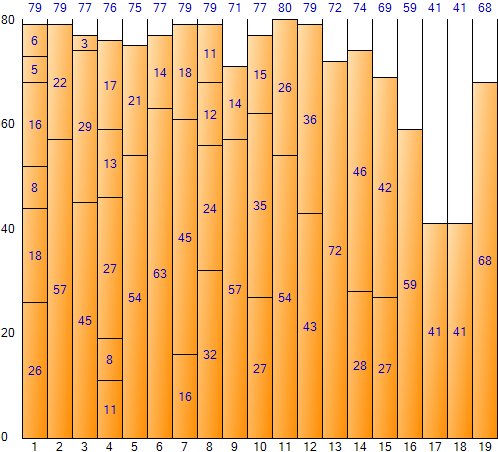
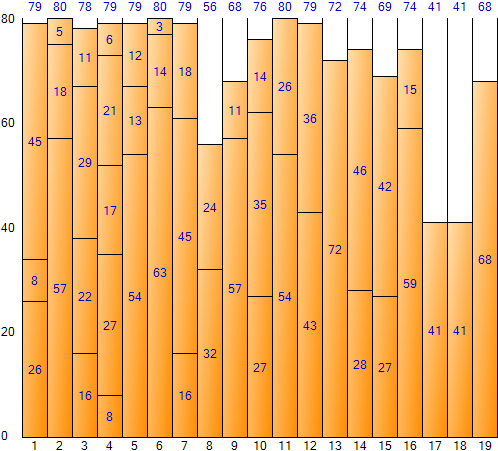
Das Ausfüllen der gesamten Eingabedaten auf diese Weise ergibt das folgende Ergebnis: (Ergebnisbildschirm der Bin-Packing-Beispielanwendung)
Die First-Fit-Methode hat den Vorteil, dass weniger Platz verschwendet wird als bei der Next-Fit-Methode, und dass aufgrund weniger Behälter insgesamt weniger Platz zur Verfügung steht. Der Nachteil ist jedoch, dass die Ausführungszeit aufgrund der relativ großen Anzahl von Iterationen lang ist. Der Gesamtplatz beträgt 1.520 (Größe 80 pro Fach * Anzahl der Fächer 19), der verbleibende Gesamtplatz beträgt 168, und die Platzineffizienz beträgt etwa 11,051 TP2T (168/1.520).
2.4. Worst-Fit-Algorithmus
Füllen Sie für jeden Artikel den Behälter, der von allen Behältern mit der größten verbleibenden Größe gefüllt werden kann, und wenn es keinen geeigneten Behälter gibt, wird ein neuer Behälter erstellt und gefüllt.
// Pseudo code
item(1)을 새로운 Bin(1)에 채운다;
for (i=2; i<=item갯수; i++) {
long lMaxRemainSize = 0;
long lMaxRemainSizeBinIndex = 0;
for (j=1; j<=Bin갯수: j++) {
// 남은공간Size가 가장 큰 Bin 탐색
if (lMaxRemainSize < Bin(j).남은공간Size) {
lMaxRemainSize = Bin(j).남은공간Size;
lMaxRemainSizeBinIndex = j;
}
}
if (item(i).Size <= Bin(lMaxRemainSizeBinIndex) {
// 남은공간Size가 가장 큰 Bin에 item(i)를 채울 수 있는 경우
Bin(lMaxRemainSizeBinIndex)에 item(i)을 채운다;
}
else {
새로운 Bin(j+1)을 생성하고 item(i)을 채운다;
}
}
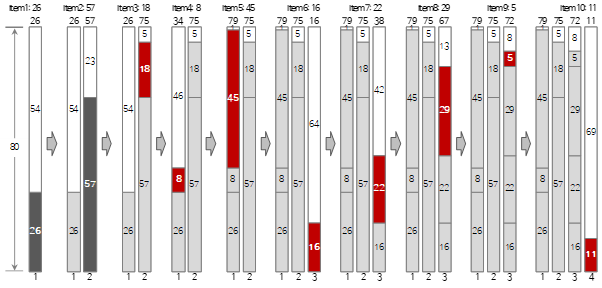
Der Vorgang des Auffüllens der ersten 10 der oben genannten Eingabedaten nach der Worst-Fit-Methode ist in der folgenden Abbildung dargestellt.
In der Abbildung zeigt das rote Element einen Fall an, in dem sich das Füllverfahren von dem First-Fit-Verfahren unterscheidet.
Das Ausfüllen der gesamten Eingabedaten auf diese Weise ergibt das folgende Ergebnis: (Ergebnisbildschirm der Bin-Packing-Beispielanwendung)
Die Worst-Fit-Methode verschwendet weniger Platz als die Next-Fit-Methode, aber mehr Platz als die First-Fit-Methode. Der Gesamtplatz beträgt 1.680 (Größe 80 pro Fach * Anzahl der Fächer 21), und der verbleibende Gesamtplatz beträgt 328, und die Platzineffizienz beträgt etwa 19,521 TP2T (328/1.680).
2.5. Best-Fit-Algorithmus
Für jeden Artikel ist es ein Verfahren, einen Behälter zu finden und zu füllen, der die kleinste verbleibende Größe unter allen Behältern hat und den entsprechenden Artikel füllen kann, und wenn es keinen geeigneten Behälter gibt, wird ein neuer Behälter erstellt und gefüllt.
// Pseudo code
for (i=2; i<=item갯수; i++) {
long lMinRemainSize = 제약조건으로 입력한 Bin의 최대 크기;
long lMinRemainSizeBinIndex = 0;
for (j=1; j<=Bin갯수: j++) {
// 남은공간Size가 가장 적으면서 item(i).Size를 채울 수 있는 Bin 탐색
if (oBin(j).남은공간Size >= item(i).SIze) and
(lMinRemainSize > oBin(j).남은공간Size)
lMinRemainSize = Bin(j).남은공간Size;
lMinRemainSizeBinIndex = j;
}
}
if (적합한 Bin을 찾았으면) {
Bin(lMinRemainSizeBinIndex)에 item(i)을 채운다;
}
else {
새로운 Bin(j+1)을 생성하고 item(i)을 채운다;
}
}
Der Vorgang des Auffüllens der ersten 10 der oben genannten Eingabedaten in der Best-Fit-Methode ist in der folgenden Abbildung dargestellt.
In der Abbildung zeigt das rote Element einen Fall an, in dem sich das Füllverfahren von dem First-Fit-Verfahren unterscheidet. Der Vergleich des Prozesses mit First Fit und Worst Fit gibt ein klares Verständnis der Methode.
Das Ausfüllen der gesamten Eingabedaten auf diese Weise ergibt das folgende Ergebnis: (Ergebnisbildschirm der Bin-Packing-Beispielanwendung)
Das Best-Fit-Verfahren erzielt im Allgemeinen die optimalsten Ergebnisse, hat jedoch den Nachteil, dass es aufgrund der großen Anzahl von Iterationen lange dauert, bis es ausgeführt wird. Der Gesamtplatz beträgt 1.520 (Größe 80 pro Fach * Anzahl der Fächer 19), der verbleibende Gesamtplatz beträgt 168, und die Platzineffizienz beträgt etwa 11,051 TP2T (168/1.520).
Das Ergebnis der First-Fit- und Best-Fit-Methoden mit der gleichen Anzahl von Bins und dem gleichen Restraum ist für die als Beispiel verwendeten Eingabedaten eindeutig und muss nicht immer gleich sein.
Wir haben uns bisher jeden Algorithmus angesehen, und als nächstes werden wir die Methode der Anwendung der absteigenden Sortierung und das Anwendungsergebnis jedes Algorithmus vergleichen.
<< Liste verwandter Artikel >>
- Optimierung der Arbeitsverteilung durch eindimensionalen Bin-Packing-Algorithmus_1.Überblick
- Optimierung der Arbeitsverteilung durch eindimensionalen Bin-Packing-Algorithmus_2.Algorithmus (1)
- Optimierung der Arbeitsverteilung mit eindimensionalem Bin-Packing-Algorithmus_2.Algorithmus(2)
- Optimierung der Arbeitsverteilung durch eindimensionalen Bin-Packing-Algorithmus_3.Implementierung (1)
- Optimierung der Arbeitsverteilung durch eindimensionalen Bin-Packing-Algorithmus_3.Implementierung (2)
- Optimierung der Arbeitsverteilung durch eindimensionalen Bin-Packing-Algorithmus_4.Attachment
- Letzte Änderungen am eindimensionalen Bin-Packing-Tool (Stand: 21. März 2021)
- Tool zur Optimierung der Arbeitsverteilung mit eindimensionalem Bin-Packing-Algorithmus Vollständiger Inhalt, Download