Optimierung der Arbeitsverteilung durch eindimensionalen Bin-Packing-Algorithmus_1.Überblick
In diesem Artikel werden wir uns das Konzept und den Algorithmus des eindimensionalen Bin Packing ansehen und herausfinden, wie man es mit dem Ziel der minimalen Anzahl von Arbeitsgruppen und der minimalen Ausführungszeit optimieren kann, es zu verwenden. Darüber hinaus werde ich das eindimensionale Bin Packing-Tool vorstellen, das ich direkt mit Excel VBA implementiert habe, und den Fall der Verwendung des in Python bereitgestellten Pakets betrachten.
Den Quellcode des in Excel VBA implementierten Tools und in Python implementierte Beispiele finden Sie unter dem folgenden Link.
Verknüpfung: https://github.com/DAToolset/1D-bin-packing
1. Überblick über den Optimierungsalgorithmus Eindimensionales Bin-Packing
1.1. Die Notwendigkeit der Behälterverpackung
Betrachten Sie den folgenden Fall.
Fall 1)
Es ist eine Umgebung mit den Datenbankservern A und B. A ist ein Server, der etwa 3.000 Tabellen verwaltet und derzeit ausgeführt wird, und B ist ein neu erstellter und leerer Server. Server A hat insgesamt 6 TB an Daten. Wir wollen die Zieltabellendaten innerhalb einer begrenzten Zeit (z. B. 6 Stunden) von Server A extrahieren und an Server B liefern. Um die Datenextraktion so schnell wie möglich abzuschließen, in wie viele Gruppen sollten die Tabellen unterteilt werden und welche Tabellen sollten in jeder Gruppe platziert werden, um das gewünschte Ergebnis zu erzielen? Diese Aufgabe sollte regelmäßig ausgeführt werden, mindestens einmal im Monat. Für jede Ausführung kann dem Server A eine neue Tabelle hinzugefügt werden, und die Datenmenge in jeder Tabelle kann erhöht oder verringert werden.
Fall 2)
Es gibt ungefähr 5.000 Jobs (Prozedur oder SQL usw.). Unter der Annahme, dass es keine Reihenfolge oder Abhängigkeit der einzelnen Jobs gibt, um die Gesamtausführungszeit zu minimieren, wie viele Gruppen sollten die Jobs aufgeteilt werden und welche Jobs sollten in welche Gruppe platziert werden?
Wie im obigen Fall erfordert das manuelle Finden der optimalen Kombination aus Hunderten oder Tausenden von Elementen einen erheblichen Zeit- und Arbeitsaufwand. Auch wenn Sie manuell eine Kombination von Aufgabengruppen finden, ist es nicht einfach zu überprüfen, ob die Kombination optimal ist.
Der Grund, warum der Bin-Packing-Algorithmus benötigt wird, sind wirtschaftliche Gründe, die mit minimaler Investition maximale Wirkung erzielen. Der Bin-Packing-Algorithmus kann universell eingesetzt werden, wenn es darum geht, die optimale Kombination zu finden, die innerhalb einer begrenzten Zeit oder innerhalb eines begrenzten Raums so viel wie möglich gefüllt werden kann.
1.2. Behälterverpackungskonzept
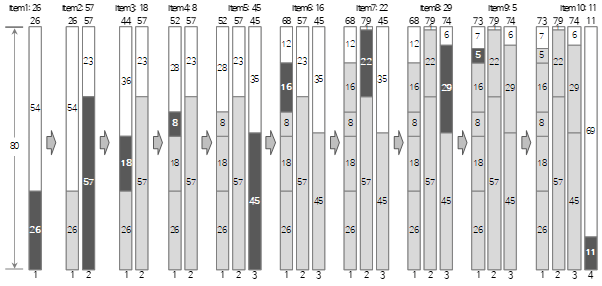
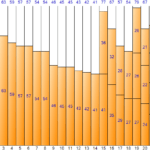
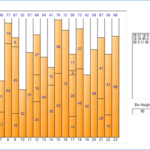
Bin Packing ist ein Optimierungsalgorithmus, der herausfindet, wie viele Behälter benötigt werden, um einen Behälter mit so vielen Artikeln wie möglich zu füllen. Es gibt zwei Eingabewerte. Das erste ist die Größe eines Behälters und das zweite ist eine Liste von Elementen. Die Liste der Artikel besteht aus einem Namen und einer Größe, und der Name wird optional eingegeben. Der Ausgabewert ist die Anzahl der optimierten (geringsten) Bins und eine Liste von Artikeln, die in jedem Bin enthalten sein sollen.
Im obigen Beispielfall 1 kann die Anzahl der Bytes der Tabelle, die Anzahl der Zeilen oder die durchschnittliche Zeit, die zum Extrahieren der Daten jeder Tabelle bei mehrfacher Ausführung benötigt wird, als Größe angesehen werden, im Fall 2 die durchschnittliche Ausführung Zeit jedes Jobs kann als Größe angesehen werden
Schauen wir uns die Bedeutung von "um die Gesamtausführungszeit zu minimieren" in Fall 2 genauer an. Die Gesamtausführungszeit ist die gleiche wie die längste Ausführungszeit unter den Ausführungszeiten der Jobgruppe, in der jeder Job platziert ist.
Das heißt, die Gesamtausführungszeit = Max (Einzelausführungszeit der Auftragsgruppe). Mit anderen Worten, da die Gesamtausführungszeit minimiert werden kann, wenn der Unterschied in der Ausführungszeit jeder Auftragsgruppe gering ist, ist "die Gesamtausführungszeit zu minimieren" dasselbe wie "die individuelle Ausführungszeit jeder Auftragsgruppe nahezu gleich zu machen". “.
Wenn die Größe eines Behälters und die Größe eines Artikels in einer quantitativen Zahl wie Länge und Zeit ausgedrückt werden können, kann die 1-dimensionale Behälterverpackung angewendet werden. Das eindimensionale Behälterpacken ist ein Algorithmus, der Artikel unterschiedlicher Größe empfängt und die maximale Größe eines Behälters als eine Beschränkung verwendet, um eine Ergebnisliste zu erhalten, indem jeder Artikel gemäß der Beschränkung angeordnet wird. Die Konzepte von Eingabe, Beschränkung und Ausgabe werden unten zusammengefasst.
- Eingabe: Eine Liste mit dem Namen und der Größe jedes Elements
- Einschränkung: Maximale Größe eines Behälters
- Ausgabe: die Anzahl der erforderlichen Behälter, eine Liste der Artikel, die jeder Behälter enthält
2-dimensionale Behälterverpackung, wenn die Größe in zwei Zahlen (Breite, Höhe) ausgedrückt werden kann, und 3-dimensionale Behälterverpackung, wenn sie in drei Zahlen (Breite, Höhe, Höhe) ausgedrückt werden kann 2D Bin Packing kann beim Anordnen oder Ausschneiden von Formen angewendet werden, um Leerraum auf einer 2D-Ebene zu minimieren. 3D Bin Packing kann angewendet werden, wenn Sie Artikel in einem 3D-Raum mit weniger Leerraum stapeln möchten. Ein typischer Fall, in dem die dreidimensionale Behälterverpackung angewendet werden kann, ist die Raumoptimierung, bei der der verbleibende Raum minimiert wird, wenn Kisten in ein Lieferfahrzeug geladen werden. 2- und 3D-Bin-Packing wird in diesem Artikel nicht behandelt.
Wir werden mehr Details im nächsten Artikel sehen.
Optimierung der Arbeitsverteilung durch eindimensionalen Bin-Packing-Algorithmus_2.Algorithmus (1)
<< Liste verwandter Artikel >>
- Optimierung der Arbeitsverteilung durch eindimensionalen Bin-Packing-Algorithmus_1.Überblick
- Optimierung der Arbeitsverteilung durch eindimensionalen Bin-Packing-Algorithmus_2.Algorithmus (1)
- Optimierung der Arbeitsverteilung mit eindimensionalem Bin-Packing-Algorithmus_2.Algorithmus(2)
- Optimierung der Arbeitsverteilung durch eindimensionalen Bin-Packing-Algorithmus_3.Implementierung (1)
- Optimierung der Arbeitsverteilung durch eindimensionalen Bin-Packing-Algorithmus_3.Implementierung (2)
- Optimierung der Arbeitsverteilung durch eindimensionalen Bin-Packing-Algorithmus_4.Attachment
- Letzte Änderungen am eindimensionalen Bin-Packing-Tool (Stand: 21. März 2021)
- Tool zur Optimierung der Arbeitsverteilung mit eindimensionalem Bin-Packing-Algorithmus Vollständiger Inhalt, Download