Optimierung der Arbeitsverteilung mit eindimensionalem Bin-Packing-Algorithmus_2.Algorithmus(2)
2.6. Absteigende Sortierung nach Artikelgröße anwenden
Bisher wurden das Betriebsverfahren und die Ausführungsergebnisse jedes Algorithmus von Next Fit, First Fit, Worst Fit und Best Fit überprüft. Wenn die Größe der Eingabedaten in einer zufälligen Reihenfolge verarbeitet wird, wenn die Größe der Eingabedaten nicht in einer bestimmten Reihenfolge angeordnet ist, ist das Ergebnis anders, wenn die Verarbeitung im sortierten Zustand erfolgt. Größere Artikel zuerst zu füllen führt in der Regel zu guten Ergebnissen, sodass Sie darüber nachdenken können, sie absteigend nach Größe der Artikel zu sortieren und zuerst zu verarbeiten.
Zunächst sind die Eingabedaten und die in absteigender Reihenfolge sortierten Daten wie folgt.
# Eingangsdaten 26 57 18 8 45 16 22 29 5 11 8 27 54 13 17 21 63 14 16 45 6 32 57 24 18 27 54 35 12 43 36 72 14 28 3 11 46 27 42 159 25 8# Eingabedaten absteigend sortieren 72 68 63 59 57 57 54 54 46 45 45 43 42 41 41 36 35 32 29 28 27 27 27 26 26 24 22 21 18 18 17 16 16 15 14 14 13 1 6 1 8. 1 6 1Sehen wir uns die Ergebnisse der Ausführung jedes Algorithmus mit den in absteigender Reihenfolge sortierten Daten als Eingabe an.
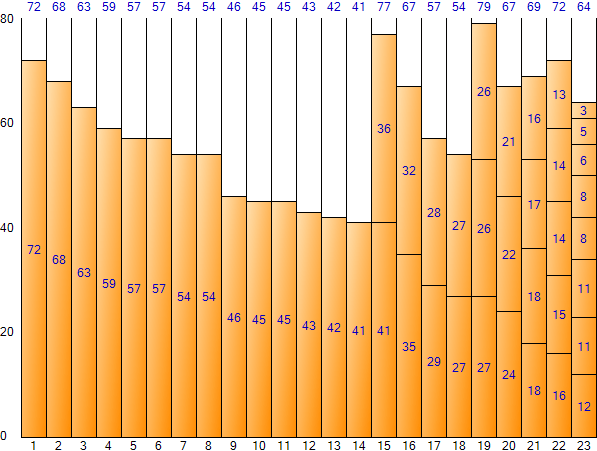
2.7. Next Fit mit absteigender Sortierung
Der Gesamtplatz beträgt 1.840 (Größe 80 pro Fach * Anzahl der Fächer 23), und der verbleibende Gesamtplatz beträgt 488, und die Platzineffizienz beträgt etwa 26,521 TP2T (488/1.840).
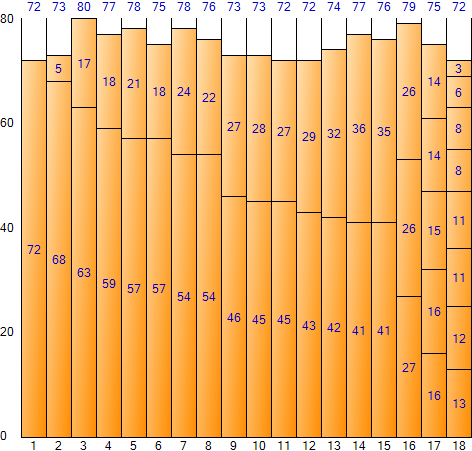
2.8. First Fit mit absteigender Sortierung
Der Gesamtplatz beträgt 1.440 (Größe 80 pro Fach * Anzahl der Fächer 18), und der verbleibende Gesamtplatz beträgt 88, und die Platzineffizienz beträgt etwa 6,111 TP2T (88/1.440).
2.9. Am schlechtesten geeignet mit absteigender Sortierung
Der Gesamtplatz beträgt 1.440 (Größe 80 pro Fach * Anzahl der Fächer 18), und der verbleibende Gesamtplatz beträgt 88, und die Platzineffizienz beträgt etwa 6,111 TP2T (88/1.440).
2.10. Beste Anpassung mit absteigender Sortierung
Der Gesamtplatz beträgt 1.440 (Größe 80 pro Fach * Anzahl der Fächer 18), und der verbleibende Gesamtplatz beträgt 88, und die Platzineffizienz beträgt etwa 6,111 TP2T (88/1.440).
2.11. Vergleich der Ergebnisse der Algorithmusanwendung
In dem oben betrachteten Fall, mit Ausnahme von Next Fit, das die größte Ineffizienz aufweist, ergaben die restliche räumliche Summe und die Raumineffizienz von First Fit, Worst Fit und Best Fit dieselben Ergebnisse, und die in jeden Behälter gefüllten Elemente waren unterschiedlich konfiguriert .
Beachten Sie, dass das gleiche Ergebnis in diesem Fall eine Koinzidenz basierend auf den Eingabedaten und Einschränkungen ist. Wenn die Eingabedaten und Beschränkungen unterschiedlich sind, können die verbleibende räumliche Summe, die Platzineffizienz und die Elementzusammensetzungsliste von Behältern unterschiedlich sein.
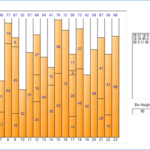
Das Vergleichen des unsortierten Ergebnisses mit dem sortierten Ergebnis ist wie folgt.
▼ Nächste Anpassung
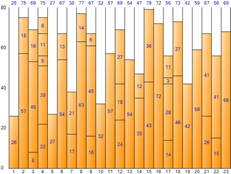
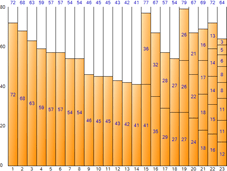
▼ Erstanpassung
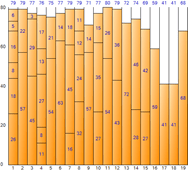
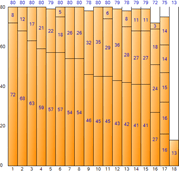
▼ Schlechteste Passform
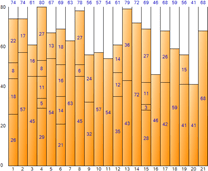
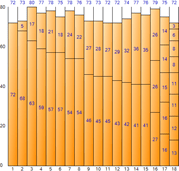
▼ Beste Passform
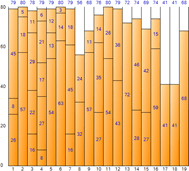
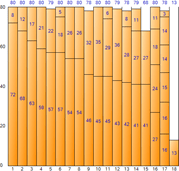
Nachfolgend finden Sie die quantitativen Informationen, die durch die Ausführung jedes Algorithmus erzeugt werden.
| Algorithmus | Artikel | vor dem Sortieren | nach Sortierung | vergleichen |
| Nächste Passform | Anzahl Vergleiche | 44 | 44 | Keine Änderung |
| ganzen Raum | 1,840 | 1,840 | ||
| Gesamter verbleibender Speicherplatz | 488 | 488 | ||
| Platzineffizienz | 26.525 | 26.525 | ||
| Erster Fit | Anzahl Vergleiche | 330 | 448 | Die Anzahl der Vergleiche nahm zu, aber die Platzineffizienz nahm ab und verbesserte sich |
| ganzen Raum | 1,520 | 1,440 | ||
| Gesamter verbleibender Speicherplatz | 168 | 88 | ||
| Platzineffizienz | 11.05% | 6.11% | ||
| Schlechteste Passform | Anzahl Vergleiche | 465 | 643 | |
| ganzen Raum | 1,680 | 1,440 | ||
| Gesamter verbleibender Speicherplatz | 328 | 88 | ||
| Platzineffizienz | 19.52% | 6.11% | ||
| Beste Passform | Anzahl Vergleiche | 428 | 643 | |
| ganzen Raum | 1,520 | 1,440 | ||
| Gesamter verbleibender Speicherplatz | 168 | 88 | ||
| Platzineffizienz | 11.05% | 6.11% |
In der obigen Tabelle wird die Anzahl der Vergleiche grob durch das Excel VBA-basierte Tool gemessen, das als nächstes vorgestellt wird. Wenn Sie sich das Obige ansehen, können Sie sehen, dass das Ergebnis der Ausführung von Bin Packing nach dem Sortieren in absteigender Reihenfolge nach Artikelgröße die Platzineffizienz reduziert und dichter füllt. Es ist ersichtlich, dass das Sortieren zuerst und das Anwenden des Algorithmus optimiertere Ergebnisse erzielen kann.
Best Fit ist nicht immer optimal. Es ist wünschenswert, die Ausführungsergebnisse jedes Algorithmus zu überprüfen und das optimale Ergebnis für jede Situation auszuwählen.
Bisher haben wir uns den Bin-Packing-Algorithmus im Detail angesehen. Als Nächstes sehen wir uns die Tools an, die diesen Algorithmus implementieren.
<< Liste verwandter Artikel >>
- Optimierung der Arbeitsverteilung durch eindimensionalen Bin-Packing-Algorithmus_1.Überblick
- Optimierung der Arbeitsverteilung durch eindimensionalen Bin-Packing-Algorithmus_2.Algorithmus (1)
- Optimierung der Arbeitsverteilung mit eindimensionalem Bin-Packing-Algorithmus_2.Algorithmus(2)
- Optimierung der Arbeitsverteilung durch eindimensionalen Bin-Packing-Algorithmus_3.Implementierung (1)
- Optimierung der Arbeitsverteilung durch eindimensionalen Bin-Packing-Algorithmus_3.Implementierung (2)
- Optimierung der Arbeitsverteilung durch eindimensionalen Bin-Packing-Algorithmus_4.Attachment
- Letzte Änderungen am eindimensionalen Bin-Packing-Tool (Stand: 21. März 2021)
- Tool zur Optimierung der Arbeitsverteilung mit eindimensionalem Bin-Packing-Algorithmus Vollständiger Inhalt, Download






Hallo, ich schaue mir Daten zum Müllverpacken an. Kann ich einige Bilder teilen?
Ja es ist ok.
Bitte hinterlassen Sie einen Kommentar und teilen Sie uns mit, wo Sie ihn teilen, und geben Sie unbedingt die Quelle an.