生产力技能

元思维，元工作

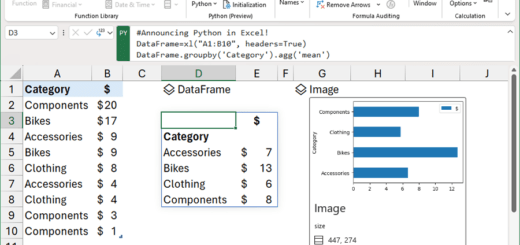
使用一维装箱算法优化工作分配_3.实现（二）

发布日期 · 已更新

3.2.使用Python Bin Packing包

3.2.1. Python Bin Packing包的介绍和安装

可以在 Python 中使用的 Bin Packing 包可以在 Pypi（Python 包索引）网页上找到。 https://pypi.python.org/pypi/bin-packing-problem/1.0.0 由...提供在这个URL中，您可以参考Bin Packing包的简要说明和示例源代码，并且可以通过下载包文件来查看实现的源代码。

bin-packing-problem 1.0.0 package
装箱问题 1.0.0 包

在该包的Fit模块中，提供了如下实现Bin Packing的方法。

算法方法（不应用排序）方法（应用排序）
下一次适合NF–（v1.0 中未实现）
首次适配FFFFD
最差拟合工作组世界粮食计划署
最合适男朋友博德

要进行安装，请使用 Python 包管理器 pip，如下所示。

pip install bin-packing-问题

3.2.2. Bin Packing示例源代码

以下是使用上面安装的 Bin Packing 包的示例源代码。使用了与目录 2 中 Bin Packing 算法说明中使用的相同输入值。

作为参考，我不知道这是包开发者的意图还是错误，但是nfd（next fitscending）方法没有实现，所以被注释掉了。

from binpackp import NumberBin, Fit

def print_result(fit_name, fit_result):
    print(fit_name + " Result: ", fit_result)
    for bin in fit_result.bins:
        print(bin)
    print()

bin_size = 80
fit_these = [26, 57, 18, 8, 45, 16, 22, 29, 5, 11, 8, 27, 54, 13, 17, 21, 63, 14, 16, 45, 6, 32, 57, 24, 18, 27, 54, 35, 12, 43, 36, 72, 14, 28, 3, 11, 46, 27, 42, 59, 26, 41, 15, 41, 68]

next_fit_results = Fit.nf(NumberBin, bin_size, fit_these)
first_fit_results = Fit.ff(NumberBin, bin_size, fit_these)
worst_fit_result = Fit.wf(NumberBin, bin_size, fit_these)
best_fit_result = Fit.bf(NumberBin, bin_size, fit_these)

# sorted_next_fit_results = Fit.nfd(NumberBin, bin_size, fit_these) # not implemented
sorted_first_fit_results = Fit.ffd(NumberBin, bin_size, fit_these)
sorted_worst_fit_result = Fit.wfd(NumberBin, bin_size, fit_these)
sorted_best_fit_result = Fit.bfd(NumberBin, bin_size, fit_these)

print_result("Next Fit", next_fit_results)
print_result("First Fit", first_fit_results)
print_result("Worst Fit", worst_fit_result)
print_result("Best Fit", best_fit_result)

# print_result("Next Fit With Sort", next_fit_results) # not implemented
print_result("First Fit With Sort", sorted_first_fit_results)
print_result("Worst Fit With Sort", sorted_worst_fit_result)
print_result("Best Fit With Sort", sorted_best_fit_result)

3.2.3. Bin Packing示例源代码输出

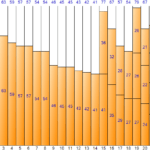
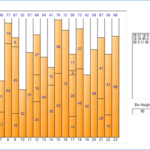
示例源码运行结果如下。虽然目录2中描述的各个算法的执行结果和输出顺序不同，但是可以看到填充的内容是相同的。

Next Fit Result:  <BPResult (Total Bins: 23, Total Volume: 1840, Unused Volume: 488)>
<NumberBin>(Volume: 26/80, Items: [26])
<NumberBin>(Volume: 75/80, Items: [57, 18])
<NumberBin>(Volume: 69/80, Items: [8, 45, 16])
<NumberBin>(Volume: 75/80, Items: [22, 29, 5, 11, 8])
<NumberBin>(Volume: 27/80, Items: [27])
<NumberBin>(Volume: 67/80, Items: [54, 13])
<NumberBin>(Volume: 38/80, Items: [17, 21])
<NumberBin>(Volume: 77/80, Items: [63, 14])
<NumberBin>(Volume: 67/80, Items: [16, 45, 6])
<NumberBin>(Volume: 32/80, Items: [32])
<NumberBin>(Volume: 57/80, Items: [57])
<NumberBin>(Volume: 69/80, Items: [24, 18, 27])
<NumberBin>(Volume: 54/80, Items: [54])
<NumberBin>(Volume: 47/80, Items: [35, 12])
<NumberBin>(Volume: 79/80, Items: [43, 36])
<NumberBin>(Volume: 72/80, Items: [72])
<NumberBin>(Volume: 56/80, Items: [14, 28, 3, 11])
<NumberBin>(Volume: 73/80, Items: [46, 27])
<NumberBin>(Volume: 42/80, Items: [42])
<NumberBin>(Volume: 59/80, Items: [59])
<NumberBin>(Volume: 67/80, Items: [26, 41])
<NumberBin>(Volume: 56/80, Items: [15, 41])
<NumberBin>(Volume: 68/80, Items: [68])

First Fit Result:  <BPResult (Total Bins: 19, Total Volume: 1520, Unused Volume: 168)>
<NumberBin>(Volume: 80/80, Items: [54, 26])
<NumberBin>(Volume: 79/80, Items: [26, 18, 8, 16, 5, 6])
<NumberBin>(Volume: 79/80, Items: [57, 22])
<NumberBin>(Volume: 77/80, Items: [45, 29, 3])
<NumberBin>(Volume: 76/80, Items: [11, 8, 27, 13, 17])
<NumberBin>(Volume: 75/80, Items: [54, 21])
<NumberBin>(Volume: 77/80, Items: [63, 14])
<NumberBin>(Volume: 79/80, Items: [16, 45, 18])
<NumberBin>(Volume: 79/80, Items: [32, 24, 12, 11])
<NumberBin>(Volume: 71/80, Items: [57, 14])
<NumberBin>(Volume: 77/80, Items: [27, 35, 15])
<NumberBin>(Volume: 79/80, Items: [43, 36])
<NumberBin>(Volume: 72/80, Items: [72])
<NumberBin>(Volume: 74/80, Items: [28, 46])
<NumberBin>(Volume: 69/80, Items: [27, 42])
<NumberBin>(Volume: 59/80, Items: [59])
<NumberBin>(Volume: 41/80, Items: [41])
<NumberBin>(Volume: 41/80, Items: [41])
<NumberBin>(Volume: 68/80, Items: [68])

Worst Fit Result:  <BPResult (Total Bins: 21, Total Volume: 1680, Unused Volume: 328)>
<NumberBin>(Volume: 80/80, Items: [29, 5, 11, 8, 27])
<NumberBin>(Volume: 41/80, Items: [41])
<NumberBin>(Volume: 46/80, Items: [46])
<NumberBin>(Volume: 54/80, Items: [54])
<NumberBin>(Volume: 56/80, Items: [41, 15])
<NumberBin>(Volume: 56/80, Items: [32, 24])
<NumberBin>(Volume: 57/80, Items: [57])
<NumberBin>(Volume: 59/80, Items: [59])
<NumberBin>(Volume: 61/80, Items: [35, 12, 14])
<NumberBin>(Volume: 61/80, Items: [45, 16])
<NumberBin>(Volume: 63/80, Items: [63])
<NumberBin>(Volume: 67/80, Items: [54, 13])
<NumberBin>(Volume: 68/80, Items: [42, 26])
<NumberBin>(Volume: 68/80, Items: [68])
<NumberBin>(Volume: 69/80, Items: [28, 3, 11, 27])
<NumberBin>(Volume: 69/80, Items: [45, 6, 18])
<NumberBin>(Volume: 72/80, Items: [72])
<NumberBin>(Volume: 74/80, Items: [57, 17])
<NumberBin>(Volume: 74/80, Items: [26, 18, 8, 22])
<NumberBin>(Volume: 78/80, Items: [21, 14, 16, 27])
<NumberBin>(Volume: 79/80, Items: [43, 36])

Best Fit Result:  <BPResult (Total Bins: 19, Total Volume: 1520, Unused Volume: 168)>
<NumberBin>(Volume: 80/80, Items: [57, 18, 5])
<NumberBin>(Volume: 80/80, Items: [63, 14, 3])
<NumberBin>(Volume: 80/80, Items: [54, 26])
<NumberBin>(Volume: 79/80, Items: [26, 8, 45])
<NumberBin>(Volume: 79/80, Items: [8, 27, 17, 21, 6])
<NumberBin>(Volume: 79/80, Items: [16, 45, 18])
<NumberBin>(Volume: 79/80, Items: [54, 13, 12])
<NumberBin>(Volume: 79/80, Items: [43, 36])
<NumberBin>(Volume: 78/80, Items: [16, 22, 29, 11])
<NumberBin>(Volume: 76/80, Items: [27, 35, 14])
<NumberBin>(Volume: 74/80, Items: [28, 46])
<NumberBin>(Volume: 74/80, Items: [59, 15])
<NumberBin>(Volume: 72/80, Items: [72])
<NumberBin>(Volume: 69/80, Items: [27, 42])
<NumberBin>(Volume: 68/80, Items: [57, 11])
<NumberBin>(Volume: 68/80, Items: [68])
<NumberBin>(Volume: 56/80, Items: [32, 24])
<NumberBin>(Volume: 41/80, Items: [41])
<NumberBin>(Volume: 41/80, Items: [41])

First Fit With Sort Result:  <BPResult (Total Bins: 18, Total Volume: 1440, Unused Volume: 88)>
<NumberBin>(Volume: 80/80, Items: [45, 35])
<NumberBin>(Volume: 80/80, Items: [54, 26])
<NumberBin>(Volume: 80/80, Items: [54, 26])
<NumberBin>(Volume: 80/80, Items: [59, 21])
<NumberBin>(Volume: 80/80, Items: [63, 17])
<NumberBin>(Volume: 80/80, Items: [68, 12])
<NumberBin>(Volume: 80/80, Items: [72, 8])
<NumberBin>(Volume: 80/80, Items: [45, 29, 6])
<NumberBin>(Volume: 80/80, Items: [57, 18, 5])
<NumberBin>(Volume: 79/80, Items: [57, 22])
<NumberBin>(Volume: 78/80, Items: [46, 32])
<NumberBin>(Volume: 79/80, Items: [43, 36])
<NumberBin>(Volume: 78/80, Items: [42, 28, 8])
<NumberBin>(Volume: 79/80, Items: [41, 27, 11])
<NumberBin>(Volume: 79/80, Items: [41, 27, 11])
<NumberBin>(Volume: 72/80, Items: [27, 24, 18, 3])
<NumberBin>(Volume: 75/80, Items: [16, 16, 15, 14, 14])
<NumberBin>(Volume: 13/80, Items: [13])

Worst Fit With Sort Result:  <BPResult (Total Bins: 18, Total Volume: 1440, Unused Volume: 88)>
<NumberBin>(Volume: 80/80, Items: [63, 17])
<NumberBin>(Volume: 72/80, Items: [13, 12, 11, 11, 8, 8, ...])
<NumberBin>(Volume: 72/80, Items: [45, 27])
<NumberBin>(Volume: 72/80, Items: [43, 29])
<NumberBin>(Volume: 72/80, Items: [72])
<NumberBin>(Volume: 73/80, Items: [68, 5])
<NumberBin>(Volume: 73/80, Items: [46, 27])
<NumberBin>(Volume: 73/80, Items: [45, 28])
<NumberBin>(Volume: 74/80, Items: [42, 32])
<NumberBin>(Volume: 75/80, Items: [16, 16, 15, 14, 14])
<NumberBin>(Volume: 75/80, Items: [57, 18])
<NumberBin>(Volume: 76/80, Items: [54, 22])
<NumberBin>(Volume: 76/80, Items: [41, 35])
<NumberBin>(Volume: 77/80, Items: [59, 18])
<NumberBin>(Volume: 77/80, Items: [41, 36])
<NumberBin>(Volume: 78/80, Items: [57, 21])
<NumberBin>(Volume: 78/80, Items: [54, 24])
<NumberBin>(Volume: 79/80, Items: [27, 26, 26])

Best Fit With Sort Result:  <BPResult (Total Bins: 18, Total Volume: 1440, Unused Volume: 88)>
<NumberBin>(Volume: 80/80, Items: [45, 35])
<NumberBin>(Volume: 80/80, Items: [54, 26])
<NumberBin>(Volume: 80/80, Items: [54, 26])
<NumberBin>(Volume: 80/80, Items: [59, 21])
<NumberBin>(Volume: 80/80, Items: [63, 17])
<NumberBin>(Volume: 80/80, Items: [68, 12])
<NumberBin>(Volume: 80/80, Items: [27, 24, 18, 11])
<NumberBin>(Volume: 80/80, Items: [72, 8])
<NumberBin>(Volume: 80/80, Items: [45, 29, 6])
<NumberBin>(Volume: 80/80, Items: [57, 18, 5])
<NumberBin>(Volume: 79/80, Items: [43, 36])
<NumberBin>(Volume: 79/80, Items: [57, 22])
<NumberBin>(Volume: 79/80, Items: [41, 27, 11])
<NumberBin>(Volume: 78/80, Items: [46, 32])
<NumberBin>(Volume: 78/80, Items: [42, 28, 8])
<NumberBin>(Volume: 78/80, Items: [16, 16, 15, 14, 14, 3])
<NumberBin>(Volume: 68/80, Items: [41, 27])
<NumberBin>(Volume: 13/80, Items: [13])

4.未来发展方向及参考资料

到目前为止，我们所了解的 Bin Packing 算法是基于每个项目是独立且彼此不相关的前提的。换句话说，它是一种不考虑依赖关系的算法，例如项目具有优先关系并且需要一起填充到一个容器中的情况。

事实上，可以说有依赖性的情况远多于无依赖性的情况。例如，在实际应用中，更常见的是Job2和Job3先执行Job1之后再执行，而不是Job1、Job2和Job3独立执行。

需要反映对迄今为止已知的装箱算法的依赖性并对其进行开发。在本文中，我们没有研究反映依赖关系的 Bin Packing。如果有人可以分享通过额外研究取得的任何改进或发展，我将非常感激。

对本文内容的反馈可以通过评论或 https://github.com/DAToolset/1D-bin-packing github问题，请发到我的邮箱。

<< 相关文章列表 >>

相关文章：

Excel VBA课程（一）：Excel VBA概述 black and white ceramic tea cup with saucer on black wooden table使用一维装箱算法的工作分配优化工具 全文, 下载 一维装箱工具近期变化（截至 2021 年 3 月 21 日） 使用一维装箱算法优化工作分配_4.附件 使用一维装箱算法优化工作分配_3.实现（一） 내림차순 정렬을 적용한 Next Fit 결과使用一维装箱算法优化工作分配_2.算法(2) 使用一维装箱算法优化工作分配_2.算法（一） 使用一维装箱算法优化工作分配_1.概述

标签：

发表回复

您的电子邮箱地址不会被公开。 必填项已用*标注

zh_CN简体中文
ko_KR한국어 en_USEnglish ja日本語 de_DEDeutsch es_ESEspañol zh_CN简体中文