使用一维装箱算法优化工作分配_2.算法(一)
2. 一维装箱算法
2.1。一维装箱算法类型
Bin Packing 的四种代表性算法如下。
- Next Fit:填写最后一个 bin 或新 bin
- First Fit:总是从第一个箱子中寻找和填充
- Worst Fit:查找并填充所有 bin 中剩余大小最大的可以填充当前 item 的 bin
- Best Fit:在所有 bin 中找到并填充可以填充当前 item 且剩余尺寸最小的 bin。
此外,通过按大小降序对整个 Item 进行排序并应用每种算法,可以获得更优化的结果。考虑到应用降序排序的方法,可以说一共有8种算法。
以下输入和约束用于解释。 (输入中项目名称省略,仅描述大小)
- 输入: 26 57 18 8 45 16 22 29 5 11 8 27 54 13 17 21 63 14 16 45 6 32 57 24 18 27 54 35 12 43 36 72 14 28 3 11 46 27 42 19 26 41 158
- 约束:80(一个容器的最大尺寸)
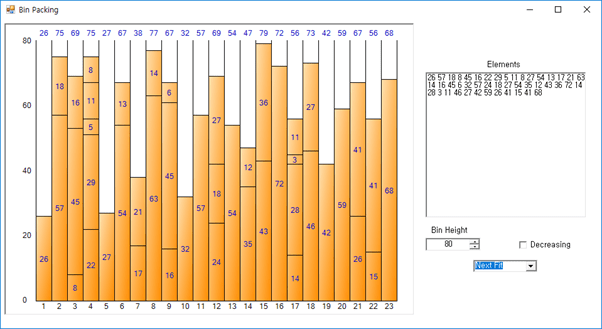
注意:此案例数据和约束是 http://www.developerfusion.com/article/5540/bin-packing/ Bin Packing Sample Application 的基本数据,可从 下载。此示例应用程序的屏幕如下所示。
下面我们来详细了解一下各个算法的伪代码、处理过程和执行结果。
2.2.下一个拟合算法
对于每个项目,如果可以填充,则填充最后一个 bin,如果无法填充,则创建并填充一个新 bin。 Next Fit 是最简单的,但结果不是最优的。
// Pseudo code
item(1)을 새로운 Bin(1)에 채운다.
for (i=2; i<=item 개수; i++) {
j = 마지막 Bin index
if (item(i).Size <= Bin(j).남은공간Size) {
Bin(j)에 item(i)를 채운다;
}
else {
새로운 Bin(j+1)을 생성하고 item(i)를 채운다;
}
}
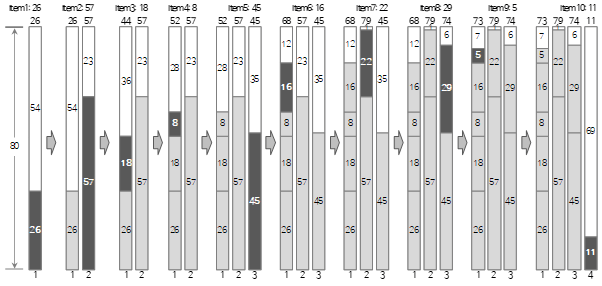
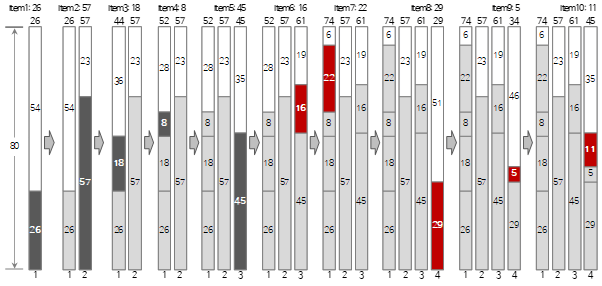
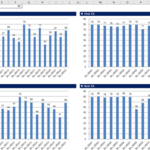
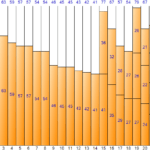
我们来看看下图中上述输入值中直到第<10>个的过程。
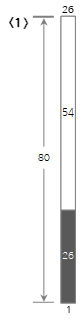
第一个输入值 <26> 创建一个新的 Bin1 并填充它。
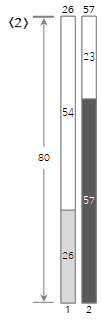
第二个输入值 <57> 大于 bin (1) 的剩余大小 (54) 并且无法填充,因此创建并填充了新的 bin (2)。
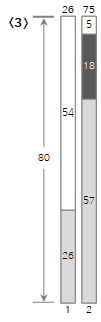
由于第三个输入值 <18> 小于当前 bin (2) 的剩余大小 (23),因此将其填充到 bin (2) 中。
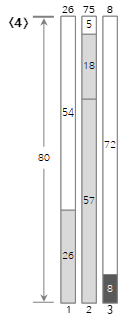
第四个输入值 <8> 大于当前 bin (2) 的剩余大小 (5) 且无法填充,因此创建并填充新的 bin (3)。正如您在此处看到的,即使 bin 中已经有剩余空间,Next Fit 方法也不会使用。因此,可能会出现大量浪费的空间。
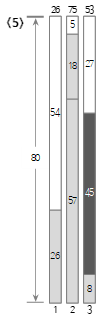
第五个输入值<45>小于当前Bin(3)的剩余大小(72),所以填充到Bin(3)中。
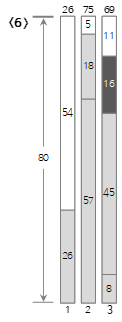
第六个输入值<16>小于当前Bin(3)的剩余大小(27),所以填充到Bin(3)中。
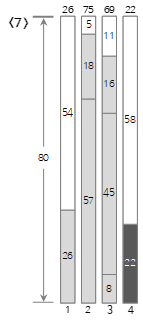
由于第七个输入值<22>大于Bin(3)(11)的剩余大小,无法填充,所以新建一个Bin(4)进行填充。
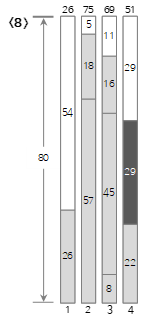
第8个输入值<29>小于当前Bin(4)的剩余大小(58),所以填充到Bin(4)中。
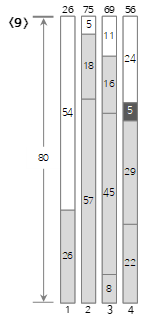
第9个输入值<5>小于当前Bin(4)的剩余大小(29),所以填充到Bin(4)中。
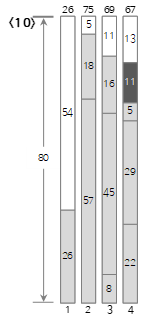
第10个输入值<11>小于当前Bin(4)的剩余大小(24),所以填充到Bin(4)中。
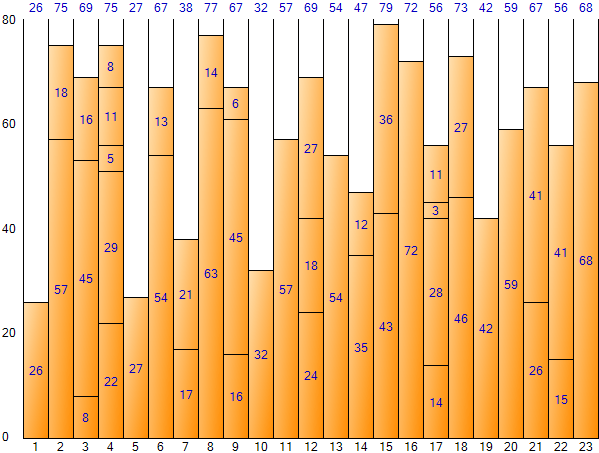
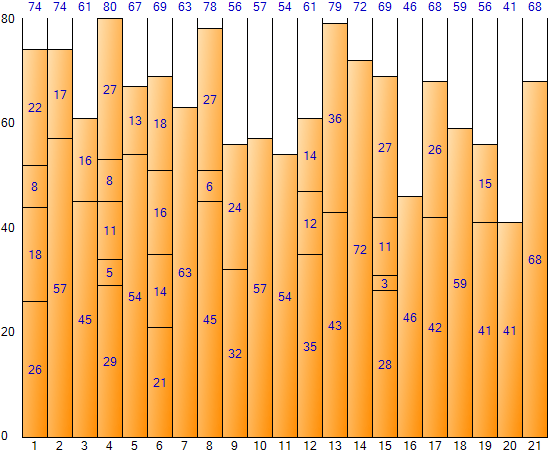
如果在 Next Fit 方法中一直填充到最后一项,可以得到如下结果。 (装箱样品申请结果画面)
如上图所示,Next Fit 方法的结果浪费了大量空间,因此很难将它们视为最优结果。但由于迭代次数少,具有执行速度快的优点。总空间为 1,840(每个 bin 的大小 80 * bin 的数量 23),剩余空间总数为 488,空间效率约为 26.52%(488/1,840)。
2.3.首次拟合算法
对于每个项目,它检查是否所有的容器都可以填充,填充第一个可以填充的容器,如果不能填充,则创建一个新的容器并填充。
// Pseudo code
item(1)을 새로운 Bin(1)에 채운다.
for (i=2; i<=item 개수; i++) {
for (j=1; j<=Bin갯수: j++) { // 항상 처음 Bin부터
if (item(i).Size <= Bin(j).남은공간Size) {
// item(i)를 채울 수 있는 Bin(j) 탐색
Bin(j)에 item(i)를 채운다;
exit for;
}
}
if (마지막 Bin까지 탐색해도 채울 수 없었으면) {
새로운 Bin(j+1)을 생성하고 item(i)를 채운다;
}
}
使用First Fit方法填充上述输入数据的前10个的过程如下图所示。
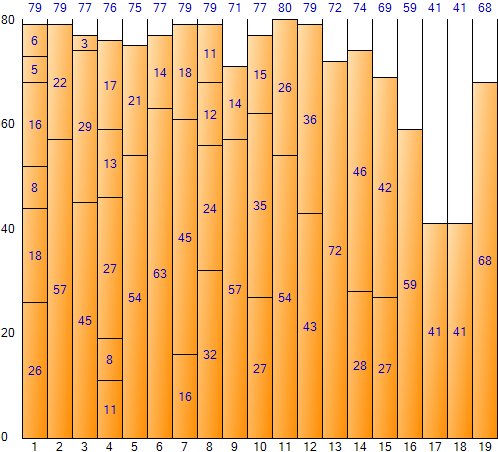
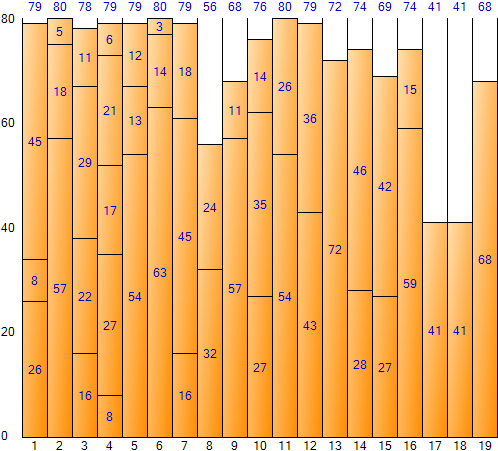
以这种方式填写整个输入数据会得到以下结果。 (装箱样品申请结果画面)
First Fit 方法比 Next Fit 具有空间更小的优势,因为它占用的空间更少,而且 bin 的数量也更少。但是它的迭代次数比较多,所以执行时间比较长。总空间为 1,520(每个 bin 的大小 80 * bin 的数量 19),剩余空间总数为 168,空间效率约为 11.05%(168/1,520)。
2.4.最差拟合算法
对于每个物品,在所有可填充的bin中填充剩余大小最大的bin,如果没有合适的bin,则创建一个新的bin并填充它。
// Pseudo code
item(1)을 새로운 Bin(1)에 채운다;
for (i=2; i<=item갯수; i++) {
long lMaxRemainSize = 0;
long lMaxRemainSizeBinIndex = 0;
for (j=1; j<=Bin갯수: j++) {
// 남은공간Size가 가장 큰 Bin 탐색
if (lMaxRemainSize < Bin(j).남은공간Size) {
lMaxRemainSize = Bin(j).남은공간Size;
lMaxRemainSizeBinIndex = j;
}
}
if (item(i).Size <= Bin(lMaxRemainSizeBinIndex) {
// 남은공간Size가 가장 큰 Bin에 item(i)를 채울 수 있는 경우
Bin(lMaxRemainSizeBinIndex)에 item(i)을 채운다;
}
else {
새로운 Bin(j+1)을 생성하고 item(i)을 채운다;
}
}
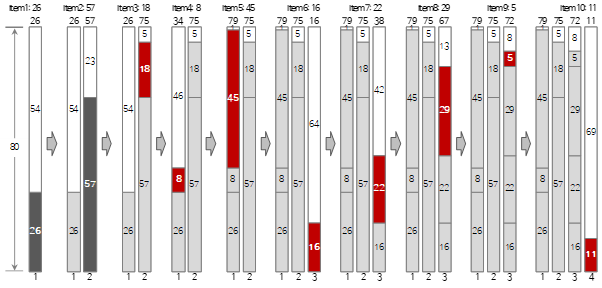
使用Worst Fit方法填充上述输入数据的前10个的过程如下图所示。
图中红色项表示First Fit方法和填充方法不同的情况。
以这种方式填写整个输入数据会得到以下结果。 (装箱样品申请结果画面)
Worst Fit 方法浪费的空间比 Next Fit 少,但比 First Fit 浪费的空间多。总空间为 1,680(每个 bin 的大小 80 * bin 的数量 21),剩余空间总数为 328,空间效率约为 19.52% (328/1,680)。
2.5.最佳拟合算法
对于每个物品,在所有的bins中,找到剩余尺寸最小的bin并填充,如果没有合适的bin,则创建一个新的bin并填充。
// Pseudo code
for (i=2; i<=item갯수; i++) {
long lMinRemainSize = 제약조건으로 입력한 Bin의 최대 크기;
long lMinRemainSizeBinIndex = 0;
for (j=1; j<=Bin갯수: j++) {
// 남은공간Size가 가장 적으면서 item(i).Size를 채울 수 있는 Bin 탐색
if (oBin(j).남은공간Size >= item(i).SIze) and
(lMinRemainSize > oBin(j).남은공간Size)
lMinRemainSize = Bin(j).남은공간Size;
lMinRemainSizeBinIndex = j;
}
}
if (적합한 Bin을 찾았으면) {
Bin(lMinRemainSizeBinIndex)에 item(i)을 채운다;
}
else {
새로운 Bin(j+1)을 생성하고 item(i)을 채운다;
}
}
使用Best Fit方法填充上述输入数据的前10个的过程如下图所示。
图中红色项表示First Fit方法和填充方法不同的情况。如果将过程与 First Fit 和 Worst Fit 进行比较,您可以清楚地理解该方法。
以这种方式填写整个输入数据会得到以下结果。 (装箱样品申请结果画面)
最佳拟合法一般会得到最优化的结果,但缺点是迭代次数多,执行时间长。总空间为 1,520(每个 bin 的大小 80 * bin 的数量 19),剩余空间总数为 168,空间效率约为 11.05%(168/1,520)。
First Fit 和 Best Fit 方法的结果具有相同数量的 bin 和相同的剩余空间这一事实对于用作示例的输入数据来说是唯一的,可能并不总是相同的。
到目前为止,我们已经了解了每种算法,接下来,我们将比较应用降序排序的方法和应用每种算法的结果。
<< 相关文章列表 >>