使用一维装箱算法优化工作分配_1.概述

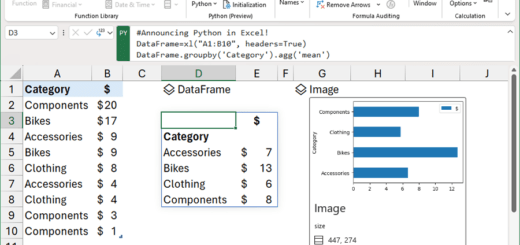
在本文中，我们将研究一维装箱的概念和算法，并了解如何以最少的工作组数和最少的执行时间为目标对其进行优化。另外介绍一下我直接用Excel VBA实现的一维装箱工具，看一下使用Python中提供的包的案例。

在 Excel VBA 中实现的工具的源代码和在 Python 中实现的示例可以在下面的链接中找到。

关联： https://github.com/DAToolset/1D-bin-packing

1. 一维装箱优化算法概述

1.1。需要装箱

考虑以下情况。

情况1）

这是一个具有数据库服务器 A 和 B 的环境。 A是管理约3000张表的服务器，目前正在运行，B是新创建的空服务器。服务器 A 总共有 6TB 的数据。我们希望在有限的时间内（例如 6 小时）从服务器 A 中提取目标表数据并将其交付给服务器 B。为了尽快完成数据抽取，应该把表格分成几组，每组放哪些表才能达到预期的效果？此任务应定期运行，至少每月一次。每次执行都可以向服务器A添加一个新表，每个表中的数据量可以增加或减少。

案例2）

大约有 5,000 个作业（过程或 SQL 等）。假设每个作业没有顺序或依赖关系，为了尽量减少整体执行时间，作业应该分成多少组，哪些作业应该放在哪一组？

与上述情况一样，人类手动尝试找到数百或数千个项目的最佳组合的过程需要花费大量时间和精力。即使人工找到了工作组的组合，要判断该组合是否最优也不是一件简单的事情。

之所以需要装箱算法，是出于经济原因，以最小的投资产生最大的效果。当需要在有限的时间或有限的空间内找到尽可能多的能被装满的最佳组合时，可以普遍使用装箱算法。

1.2. Bin 包装概念

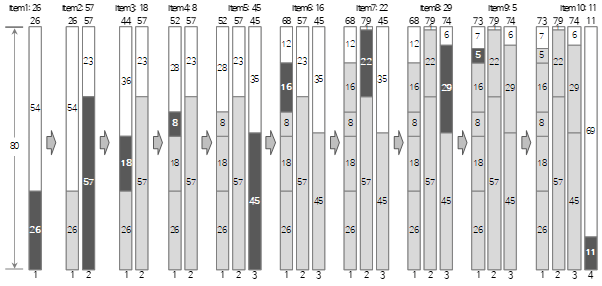
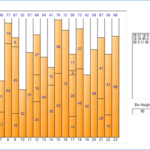
Bin Packing 是一种优化算法，它找出需要多少个 bin 才能用尽可能多的项目填充一个 bin。有两个输入值。第一个是一个 bin 的大小，第二个是项目列表。项目列表由名称和大小组成，并且可以选择输入名称。输出值是优化（最少）箱的数量和要包含在每个箱中的项目列表。

在上面的例子案例一中，表的字节数，行数，或者多次执行时提取每个表的数据的平均时间都可以看做大小。案例二中，平均执行每个作业的时间可以看作是大小。可以

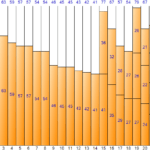
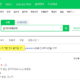
 让我们仔细看看案例 2 中“最小化总执行时间”的含义。总执行时间与放置每个作业的作业组的执行时间中最长的执行时间相同。

即总执行时间=Max（作业组个体执行时间）。换句话说，由于在每个作业组的执行时间差异较小的情况下可以最小化整体执行时间，因此“最小化整体执行时间”与“使每个作业组的单独执行时间几乎相等”相同”。

当 bin 的大小和 item 的大小可以用长度和时间等一个数量表示时，可以应用一维 bin 打包。一维装箱是一种算法，它接收各种尺寸的物品，并以一个箱的最大尺寸作为一个约束，通过根据约束对每个物品进行排列，得到一个结果列表。输入、约束和输出的概念总结如下。

• 输入：每个项目的名称和大小的列表
• 约束：一个 bin 的最大尺寸
• 输出：所需的 bin 数量，每个 bin 包含哪些项目的列表

2-Dimension Bin Packing 当尺寸可以用两个数字（宽度、高度）表示时和 3-Dimension Bin Packing 当它可以用三个数字（宽度、高度、高度）表示时适用在排列或切割形状时可以应用 2D Bin Packing 以最小化 2D 平面上的空白空间。当您想在 3D 空间中堆放物品时，可以应用 3D 装箱，而空间较少。可以应用三维装箱的典型案例是空间优化，其中在运送车辆中装载箱子时剩余空间最小化。 2 和 3D bin 包装不在本文中介绍。

我们将在下一篇文章中看到更多细节。

使用一维装箱算法优化工作分配_2.算法（一）

---

<< 相关文章列表 >>

• 使用一维装箱算法优化工作分配_1.概述
• 使用一维装箱算法优化工作分配_2.算法（一）
• 使用一维装箱算法优化工作分配_2.算法(2)
• 使用一维装箱算法优化工作分配_3.实现（一）
• 使用一维装箱算法优化工作分配_3.实现（二）
• 使用一维装箱算法优化工作分配_4.附件
• 一维装箱工具近期变化（截至 2021 年 3 月 21 日）
• 使用一维装箱算法的工作分配优化工具 全文, 下载