1次元Bin Packingアルゴリズムを活用した作業配分最適化_2.アルゴリズム(1)

2. 1次元Bin Packingアルゴリズム

2.1。 1次元Bin Packingアルゴリズムの種類

Bin Packingの4つの代表的なアルゴリズムは次のとおりです。

1. 次のフィット：最後のビンまたは新しいビンに塗りつぶす
2. First Fit：常に最初のBinからナビゲートして塗りつぶす
3. Worst Fit: 全体のビンの中で残りのサイズが最も大きく、現在アイテムを埋めることができるビンを探索して塗りつぶす
4. Best Fit：Bin全体のうち、残りのサイズが最も小さく、現在Itemを埋めることができるBinを探索して塗りつぶす 

ちなみに、Item全体をサイズ降順でソートし、各アルゴリズムを適用すると、はるかに最適化された結果が得られます。降順ソートを適用する方法まで考慮すると、合計8つのアルゴリズムがあるといえる。

説明のために、次の入力と制約を使用してください。 （入力のItem名称は省略してサイズのみ記述する）

• 入力データ：26 57 18 8 45 16 22 29 5 11 8 27 54 13 17 21 63 14 16 45 6 32 57 24 18 27 54 35 12 43 36 72 4 4
• 制約：80（Bin 1の最大サイズ）

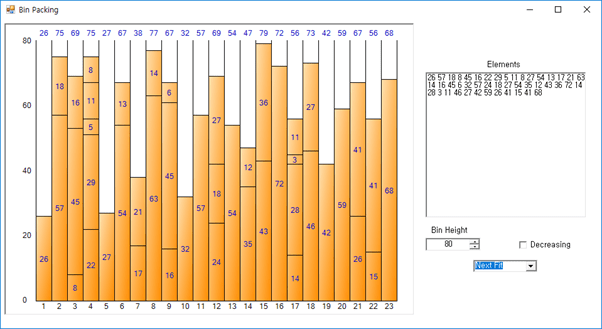
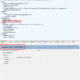
注：このケースデータと制約は http://www.developerfusion.com/article/5540/bin-packing/ からダウンロードできるBin Packing Sample Applicationの基本データをそのまま使用した。このサンプルアプリケーションの画面は次のとおりです。

各アルゴリズムの擬似コード（擬似コード）と処理過程、実行結果を詳しく見てみよう。

2.2.次のフィットアルゴリズム

各アイテムに対して最後のBinに埋めることができれば埋め、埋められないなら新しいBinを作って埋める方法だ。 Next Fitは最も簡単ですが、結果は最適とは言い難いです。

// Pseudo code
item(1)을 새로운 Bin(1)에 채운다.
for (i=2; i<=item 개수; i++) {
    j = 마지막 Bin index
    if (item(i).Size <= Bin(j).남은공간Size) {
        Bin(j)에 item(i)를 채운다;
    }
    else {
        새로운 Bin(j+1)을 생성하고 item(i)를 채운다;
    }
}

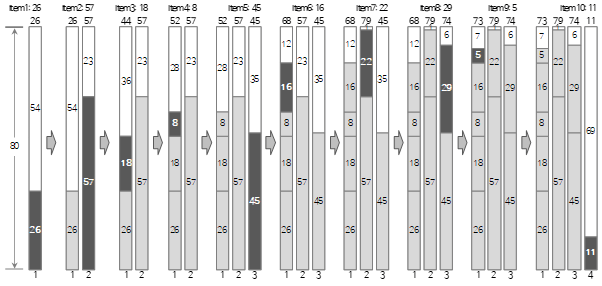
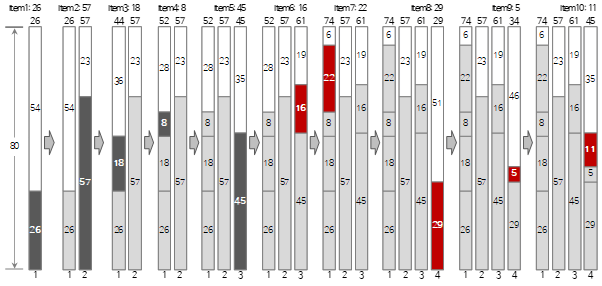
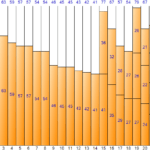
上記の入力値のうち<10>番目までの手順を下から図に見てみましょう。

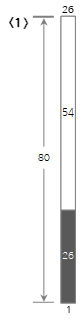
最初の入力値<26>は新しいBin1を作成し、ここに入力します。

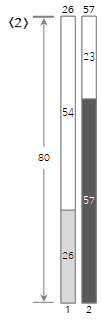
2番目の入力値<57>は、Bin（1）の残りのサイズ（54）より大きく、埋められないため、新しいBin（2）を作成して埋めます。

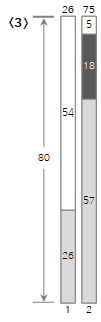
3番目の入力値<18>は、現在のBin（2）の残りのサイズ（23）より小さいため、Bin（2）に埋められます。

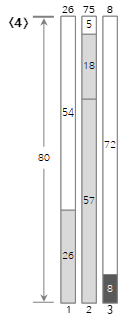
4番目の入力値<8>は、現在のBin（2）の残りのサイズ（5）よりも大きくて埋められないため、新しいBin（3）を作成して埋めます。ここでわかるように、次のフィット方法は、すでに通過したビンに残っているスペースがあっても使用しません。したがって、空間の無駄が多く発生する可能性があります。

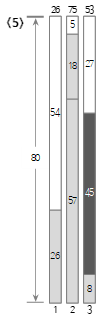
5番目の入力値<45>は、現在のBin（3）の残りのサイズ72より小さいので、Bin（3）に埋められます。

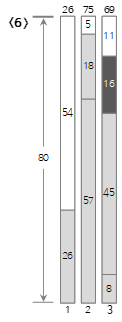
6番目の入力値<16>は、現在のBin（3）の残りのサイズ（27）より小さいため、Bin（3）に埋められます。

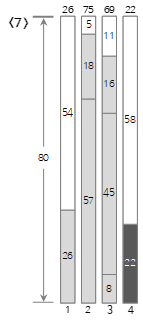
7番目の入力値<22>は、Bin（3）の残りのサイズ（11）より大きく、埋められないため、新しいBin（4）を作成して埋めます。

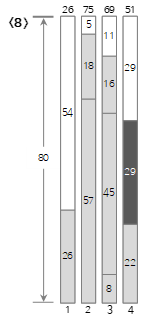
8番目の入力値<29>は、現在のBin（4）の残りのサイズ（58）より小さいため、Bin（4）に埋められます。

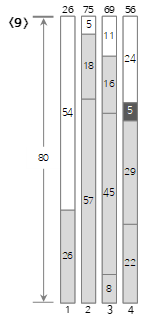
9番目の入力値<5>は、現在のBin（4）の残りのサイズ（29）より小さいため、Bin（4）に埋められます。

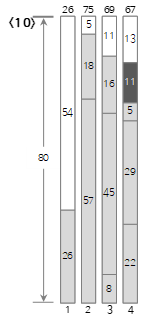
10番目の入力値<11>は、現在のBin（4）の残りのサイズ（24）より小さいため、Bin（4）に埋められます。

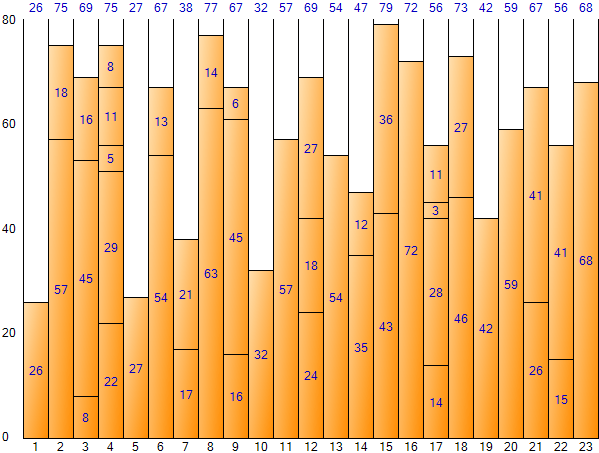
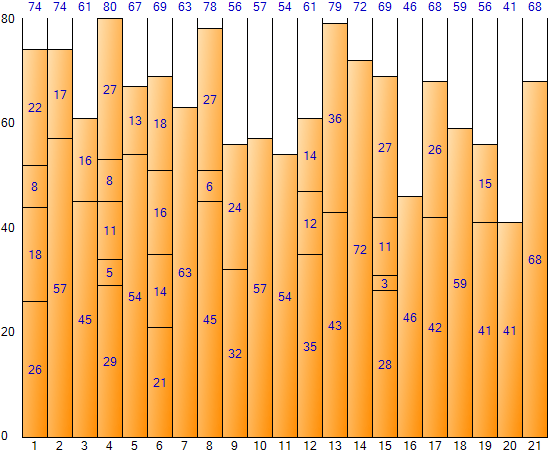
Next Fit 方式で最後の item まで続けると、次のような結果が得られる。 (Bin Packing Sample Applicationの結果画面)

Next Fit方式の結果は上図に示すように空間の無駄が大きく、最適な結果として見ることは難しい。しかし、繰り返し回数が少なくて実行速度が速いメリットがある。全空間は1,840（Bin一つ当たりサイズ80*Bin個数23）であり、残余空間合計は488で空間非効率は約26.52%（488/1,840）である。

2.3。 First Fitアルゴリズム

各 item に対して Bin 全体に塗りつぶすことができるかどうかを確認して塗りつぶすことができる最初の Bin に塗りつぶし、塗りつけられなければ新しい Bin を作って塗りつぶす方法だ。

// Pseudo code
item(1)을 새로운 Bin(1)에 채운다.
for (i=2; i<=item 개수; i++) {
    for (j=1; j<=Bin갯수: j++) { // 항상 처음 Bin부터
        if (item(i).Size <= Bin(j).남은공간Size) {
            // item(i)를 채울 수 있는 Bin(j) 탐색
            Bin(j)에 item(i)를 채운다;
            exit for;
        }
    }
    if (마지막 Bin까지 탐색해도 채울 수 없었으면) {
        새로운 Bin(j+1)을 생성하고 item(i)를 채운다;
    }
}

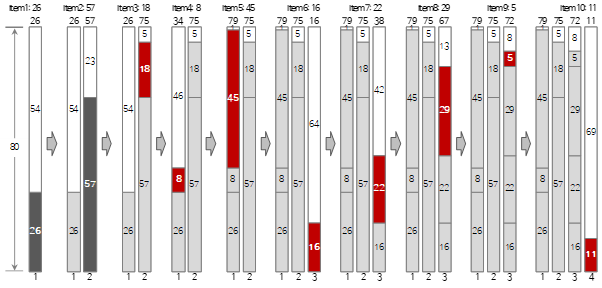
上記の入力資料のうち、First Fit方式で最初の10個まで充填する過程は、次の図のようになります。

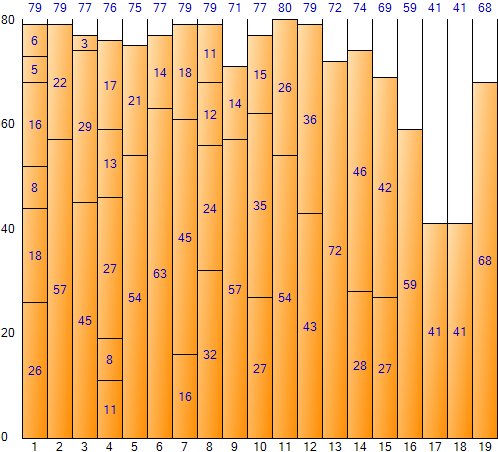
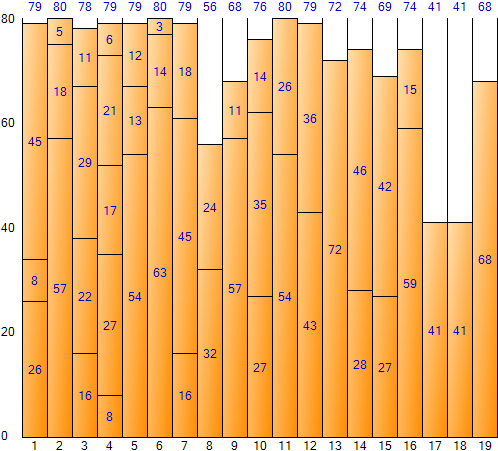
この方法で入力データ全体を埋めると、次のような結果が得られます。 (Bin Packing Sample Applicationの結果画面)

First Fit方式はNext Fitよりもスペースの無駄が少なく、Binの数が少なく、全体のスペースが小さいという利点がある。しかし、比較的繰り返し回数が多く、実行時間は長くかかるのは短所だ。全空間は1,520（Bin一つ当たりサイズ80×Bin個数19）であり、残余空間合計は168で、空間非効率は約11.05%（168/1,520）である。

2.4。 Worst Fitアルゴリズム

各アイテムに対して、すべてのBinの中で残ったサイズが最大で満たせるBinに塗り、適切なBinがなければ新しいBinを作って埋める方法だ。

// Pseudo code
item(1)을 새로운 Bin(1)에 채운다;
for (i=2; i<=item갯수; i++) {
    long lMaxRemainSize = 0;
    long lMaxRemainSizeBinIndex = 0;
    for (j=1; j<=Bin갯수: j++) {
        // 남은공간Size가 가장 큰 Bin 탐색
        if (lMaxRemainSize < Bin(j).남은공간Size) {
            lMaxRemainSize = Bin(j).남은공간Size;
            lMaxRemainSizeBinIndex = j;
        }
    }
    if (item(i).Size <= Bin(lMaxRemainSizeBinIndex) {
        // 남은공간Size가 가장 큰 Bin에 item(i)를 채울 수 있는 경우
        Bin(lMaxRemainSizeBinIndex)에 item(i)을 채운다;
    }
    else {
        새로운 Bin(j+1)을 생성하고 item(i)을 채운다;
    }
}

上記の入力資料のうち、Worst Fit方式で最初の10個まで充填する過程は、次の図の通りである。

図中の赤いアイテムは、First Fit方式と塗りつぶし方式が異なる場合を示しています。

この方法で入力データ全体を埋めると、次のような結果が得られます。 (Bin Packing Sample Applicationの結果画面)

Worst Fit方式はNext Fitよりも空間の無駄が少ないがFirst Fitよりは空間の無駄が大きい方だ。全空間は1,680（Bin一つ当たりサイズ80*Bin個数21）であり、残余空間合計は328で、空間非効率は約19.52%（328/1,680）である。

2.5。ベストフィットアルゴリズム

各アイテムについて、すべてのビンの中で残りのサイズが最も少なく、そのアイテムを埋めることができるビンを見つけて埋め、適切なビンがなければ新しいビンを作って埋める方法だ。

// Pseudo code
for (i=2; i<=item갯수; i++) {
    long lMinRemainSize = 제약조건으로 입력한 Bin의 최대 크기;
    long lMinRemainSizeBinIndex = 0;
    for (j=1; j<=Bin갯수: j++) {
        // 남은공간Size가 가장 적으면서 item(i).Size를 채울 수 있는 Bin 탐색
        if (oBin(j).남은공간Size >= item(i).SIze) and
           (lMinRemainSize > oBin(j).남은공간Size)
            lMinRemainSize = Bin(j).남은공간Size;
            lMinRemainSizeBinIndex = j;
        }
    }
    if (적합한 Bin을 찾았으면) {
        Bin(lMinRemainSizeBinIndex)에 item(i)을 채운다;
    }
    else {
        새로운 Bin(j+1)을 생성하고 item(i)을 채운다;
    }
}

上記の入力資料のうち、Best Fit方式で最初の10個まで充填する過程は、次の図の通りです。

図中の赤いアイテムは、First Fit方式と塗りつぶし方式が異なる場合を示しています。プロセスをFirst Fit、Worst Fitと比較すると、方法を確実に理解することができます。

この方法で入力データ全体を埋めると、次のような結果が得られます。 (Bin Packing Sample Applicationの結果画面)

Best Fit方式は一般に最も最適化された結果を得ることができるが、繰り返し回数が多くて実行時間が長くかかるという欠点がある。全空間は1,520（Bin一つ当たりサイズ80×Bin個数19）であり、残余空間合計は168で、空間非効率は約11.05%（168/1,520）である。

First FitとBest Fit方式の結果が同じBin個数、同じ残余空間であることは、現在の例として使用している入力資料でユニークに発生したものであり、必ずしも同じではないかもしれない。

---

ここまで各アルゴリズムについて調べて、次に降順ソートを適用する方法と各アルゴリズムの適用結果を比較します。

---

<< 関連記事のリスト >>

• 1次元Bin Packingアルゴリズムを活用した作業配分の最適化_1.概要
• 1次元Bin Packingアルゴリズムを活用した作業配分最適化_2.アルゴリズム(1)
• 1次元Bin Packingアルゴリズムを活用した作業配分最適化_2.アルゴリズム(2)
• 1次元Bin Packingアルゴリズムを活用した作業配分最適化_3.実装(1)
• 1次元Bin Packingアルゴリズムを活用した作業配分最適化_3.実装(2)
• 1次元Bin Packingアルゴリズムを活用した作業配分の最適化_4。
• 1次元Bin Packingツール最近の変更（2021-03-21基準）
• 1次元Bin Packingアルゴリズムを活用した作業配分最適化ツール