1次元Bin Packingアルゴリズムを活用した作業配分の最適化_1.概要

この記事では、1次元Bin Packingの概念とアルゴリズムについて調べて、これを利用して最小の作業グループ数と最小の実行時間を目標に最適化する方法を調べる。また、私がExcel VBAで直接実装した1次元Bin Packingツールについて紹介し、Pythonで提供されているパッケージを利用するケースについて見てみましょう。

Excel VBAで実装したツールのソースコードとPythonで実装した例は、以下のリンクで確認できます。

リンク： https://github.com/DAToolset/1D-bin-packing

1. 最適化アルゴリズム 1次元Bin Packingの概要

1.1。 Bin Packingの必要性

次のような場合を考えてみましょう。

ケース1）

DatabaseサーバーAとBがある環境です。 Aは約3000台のテーブルを管理し、現在運営されているサーバーであり、Bは新しく作られて何もなく空いているサーバーである。 Aサーバーのデータは合計6TBに達する。制約された時間（例えば、６時間）内にＡサーバの対象テーブルデータを抽出してＢサーバに渡したい。できるだけ早くデータ抽出を完了するには、テーブルをいくつかのグループに分割し、各グループにどのテーブルを配置する必要がありますか？この作業は毎月1回以上定期的に実行する必要があります。実行ごとに、Aサーバーに新しいテーブルを追加でき、各テーブルのデータ量を増減できます。

ケース2）

5000以上のJob（ProcedureやSQLなど）があります。各ジョブの順序や依存関係がない場合は、実行時間全体を最小限に抑えるために、ジョブをいくつかのグループに分割し、どのジョブをどのグループに配置する必要がありますか？

上記のケースのように、数百、数千以上のアイテムを持って最適な組み合わせを見つける過程を人が手作業で試みるには相当な時間と努力が必要である。もし手作業でどんなワークグループの組み合わせを見つけたとしても、その組み合わせが最適かどうかを確認するのはそれほど単純な問題ではない。

Bin Packingアルゴリズムが必要な理由は、最小限の投資で最大の効果を出す経済的な理由による。 Bin Packingアルゴリズムは、制約された時間内または制約されたスペース内にできるだけ多く埋めることができる最適な組み合わせを見つける必要がある場合に汎用的に使用できます。

1.2. Bin Packingのコンセプト

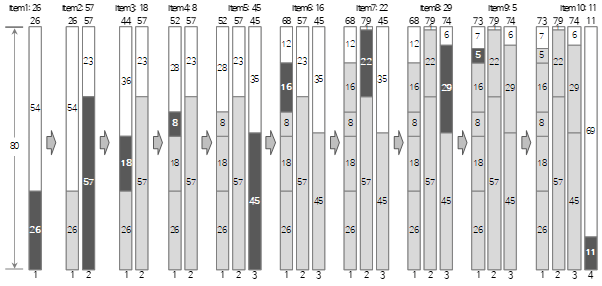
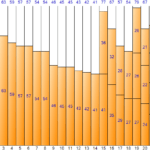
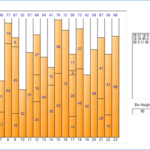
Bin Packingは、複数のアイテム（Item）をBinにできるだけ多く埋めるためにいくつのBinが必要かどうかを調べる最適化アルゴリズムです。入力値は2つあります。 1つ目は1 Binのサイズ、2つ目はItemのリストです。 Itemのリストは名前とサイズで構成され、名前はオプションで入力します。出力値は、最適化された（最も少ない）Binの数、および各Binに入れるItemのリストです。

上の例 Case 1 ではテーブルの byte 数、row 数、または複数回実行する場合、各テーブルのデータの抽出にかかった平均時間をサイズで見ることができ、 Case 2 では各 Job の平均実行時間をサイズで見るできる。

 Case 2で「全体の実行時間を最小限に抑えるには」の意味をもう少し見てみましょう。全体の実行時間は、各ジョブが配置されているジョブグループの実行時間のうち最も長くかかる実行時間と同じです。

すなわち、総実行時間＝Ｍａｘ（Ｊｏｂグループ個別実行時間）である。つまり、各ジョブグループの実行時間の差が少なくて実行時間を最小限に抑えることができるので、「全体の実行時間を最小化するには」とは、「各ジョブグループの個々の実行時間をほぼ均等にするには」と同じ意味である。

Binの大きさとItemの大きさが長さ、時間など定量的な数値で表現できる場合、1次元(1-Dimension) Bin Packingを適用することができる。 1次元Bin Packingは、さまざまなサイズのItemを入力され、Bin 1つの最大サイズを1つの制約条件として使用して、各Itemを制約条件に合わせて配置した結果リストを取得したいアルゴリズムです。入力と制約条件、出力に関する概念をまとめると以下のようになる。

• 入力：Itemそれぞれの名前とサイズのリスト
• 制約：Bin 1つの最大サイズ
• 出力：必要なビンの数、各ビンにどのアイテムが含まれるかについてのリスト

サイズが2つの数値（水平、縦）で表現できる場合は2次元（2-Dimension）Bin Packing、3つの数値（横、縦、高さ）で表現できる場合は、3次元（3-Dimension）Bin Packing適用する。 2次元Bin Packingは、2次元平面内の空きスペースが最小になるように図形を配置または切り取るときに適用できます。 3次元Bin Packingは、3次元空間に空きスペースが少ないようにアイテムを積みたい場合に適用することができる。 3次元Bin Packingを適用できる代表的な場合は、宅配車にボックスを積載する際に残るスペースが最小化されるように積載する空間最適化である。 2、3次元Bin Packingはこの記事では扱わない。

詳細については、次の記事を見てみましょう。

1次元Bin Packingアルゴリズムを活用した作業配分最適化_2.アルゴリズム(1)

---

<< 関連記事のリスト >>

• 1次元Bin Packingアルゴリズムを活用した作業配分の最適化_1.概要
• 1次元Bin Packingアルゴリズムを活用した作業配分最適化_2.アルゴリズム(1)
• 1次元Bin Packingアルゴリズムを活用した作業配分最適化_2.アルゴリズム(2)
• 1次元Bin Packingアルゴリズムを活用した作業配分最適化_3.実装(1)
• 1次元Bin Packingアルゴリズムを活用した作業配分最適化_3.実装(2)
• 1次元Bin Packingアルゴリズムを活用した作業配分の最適化_4。
• 1次元Bin Packingツール最近の変更（2021-03-21基準）
• 1次元Bin Packingアルゴリズムを活用した作業配分最適化ツール